Pairwise Maximum Likelihood

In [1]:

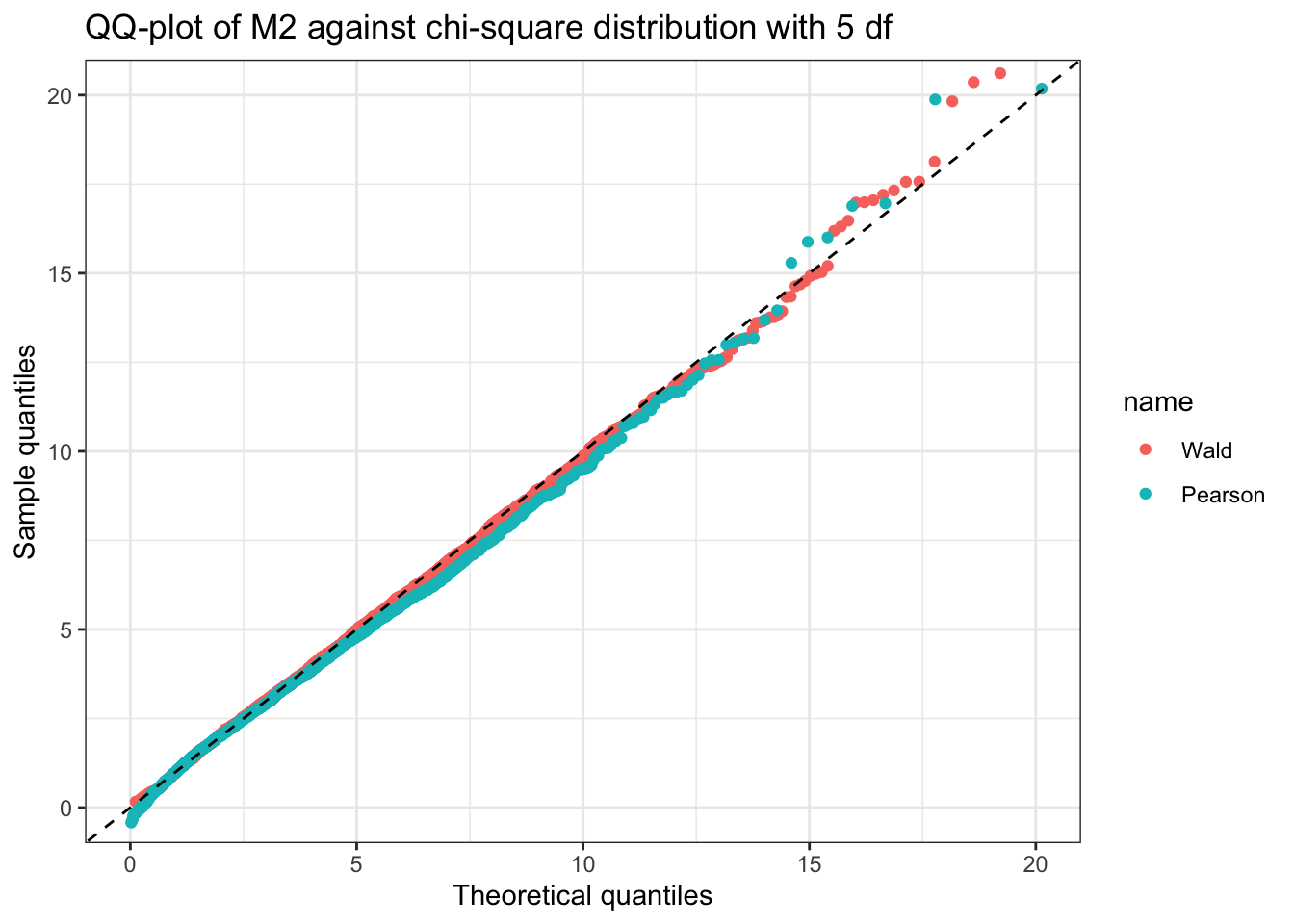
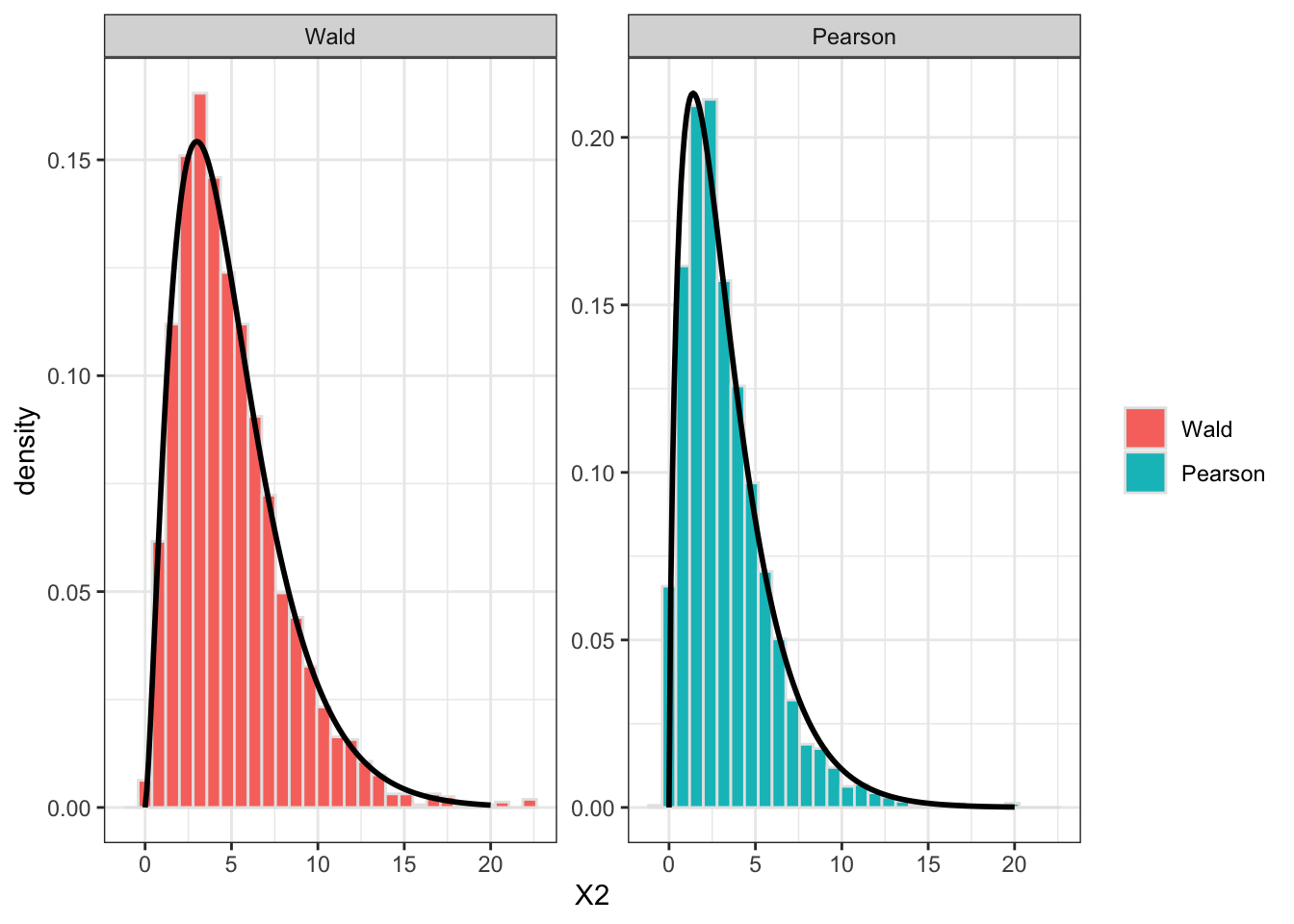
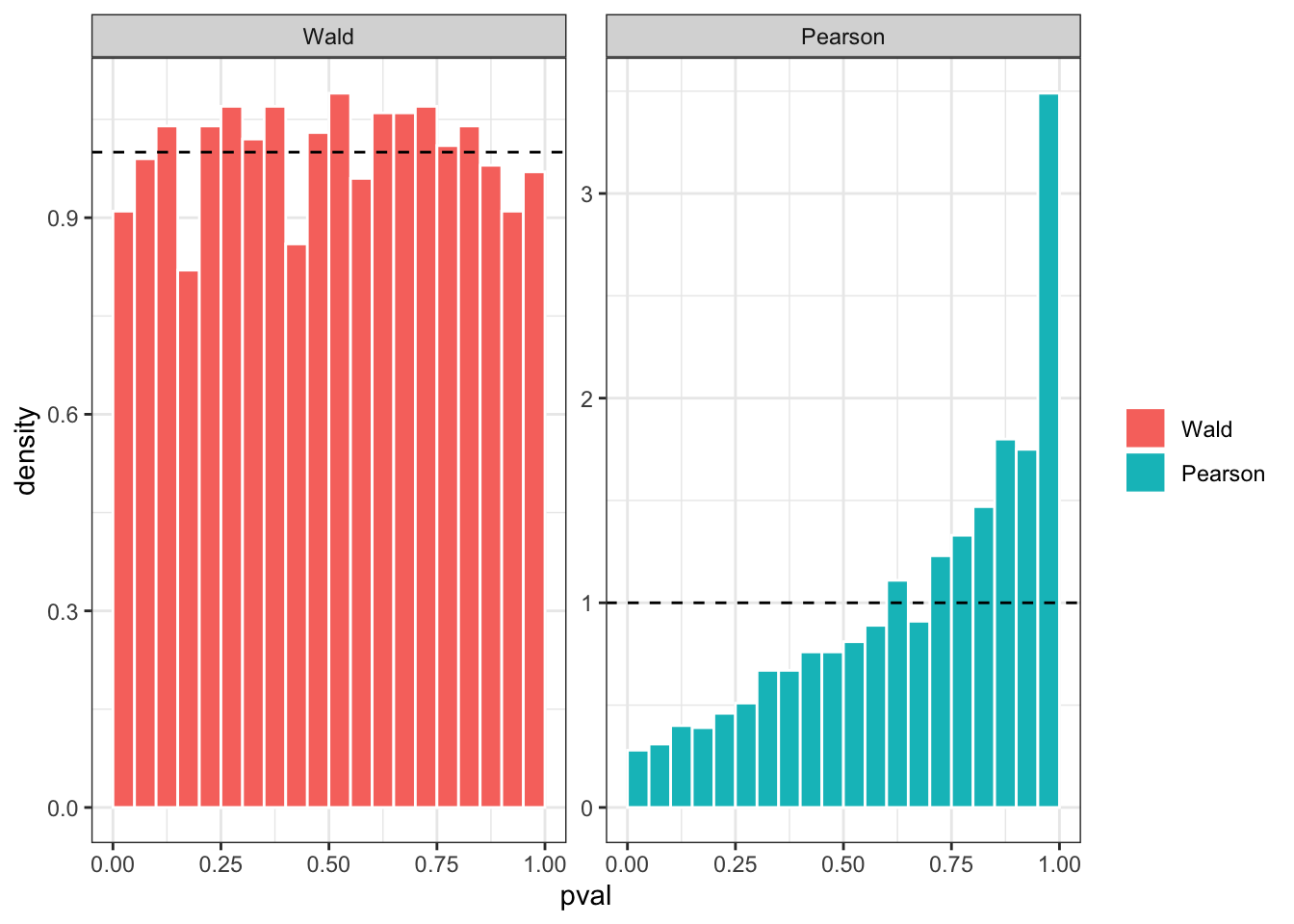
here::i_am("notebooks/pml.qmd")

here() starts at /Users/haziqj/github_local/ligof-tests

source(here::here("notebooks/ligof.R"))

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.2     ✔ tibble    3.3.0
✔ lubridate 1.9.4     ✔ tidyr     1.3.1
✔ purrr     1.0.4     

── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
This is lavaan 0.6-19
lavaan is FREE software! Please report any bugs.

Rows: 1,000
Columns: 5
$ y1 <ord> 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 1, 1, 2, 2, 2, 2, 2, 2, 2…
$ y2 <ord> 2, 1, 2, 1, 2, 1, 1, 2, 2, 2, 2, 1, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1, 2…
$ y3 <ord> 1, 2, 1, 2, 1, 1, 1, 1, 1, 2, 2, 1, 2, 1, 2, 2, 2, 1, 2, 2, 2, 2, 1…
$ y4 <ord> 2, 2, 2, 2, 2, 2, 1, 2, 2, 1, 2, 1, 2, 1, 1, 2, 2, 2, 2, 2, 2, 1, 2…
$ y5 <ord> 2, 2, 1, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2…
 num [1:15] 1.11e-16 -2.22e-16 0.00 0.00 0.00 ...

We can use the estimator = "PML" argument in {lavaan} to fit a model using pairwise maximum likelihood (PML) estimation.

In [2]:

fit <- cfa("f1 =~ y1 + y2 + y3 + y4 + y5", data = dat, estimator = "PML", 
           std.lv = TRUE)
coef(fit)

f1=~y1 f1=~y2 f1=~y3 f1=~y4 f1=~y5  y1|t1  y2|t1  y3|t1  y4|t1  y5|t1 
 0.681  0.716  0.411  0.407  0.291 -1.433 -0.490 -0.045 -0.723 -1.049 

Alternatively, we can use the addon package {lavaan.pl} for more efficient PML estimation.

In [3]:

library(lavaan.pl)

ℹ Loading required package: lavaan
── Conflicts ─────────────────────────────────────────── lavaan.pl 0.1.0.9002 ──
✖ lavaan.pl::cfa() masks lavaan::cfa()

Attaching package: 'lavaan.pl'


The following object is masked from 'package:lavaan':

    cfa

# fit <- lavaan.pl::cfa("f1 =~ y1 + y2 + y3 + y4 + y5", data = dat, std.lv = TRUE)
coef(fit)

f1=~y1 f1=~y2 f1=~y3 f1=~y4 f1=~y5  y1|t1  y2|t1  y3|t1  y4|t1  y5|t1 
 0.681  0.716  0.411  0.407  0.291 -1.433 -0.490 -0.045 -0.723 -1.049 

\(\mathbf T_2\) matrix

This is the design matrix that maps all joint probabilities to univariate and bivariate moments.

In [4]:

CREATE_T2_MAT <- function(m) {
  # m: integer vector of length p, where m[i] = number of categories of variable i
  p <- length(m)
  # 1) all joint patterns (rows = ∏ m[i], cols = p)
  patterns <- expand.grid(rev(lapply(m, seq_len)), KEEP.OUT.ATTRS = FALSE, stringsAsFactors = FALSE)
  patterns <- patterns[, rev(seq_len(p))] # reverse to match y1, y2, ...
  n_pat <- nrow(patterns)
  
  # 2) precompute total number of rows: sum_i (m[i]-1) + sum_{i<j} (m[i]-1)*(m[j]-1)
  uni_rows <- sum(m - 1)
  biv_rows <- 0L
  for(i in seq_len(p-1)) for(j in (i+1):p)
    biv_rows <- biv_rows + (m[i]-1)*(m[j]-1)
  total_rows <- uni_rows + biv_rows
  
  # 3) allocate
  out <- matrix(0L, nrow = total_rows, ncol = n_pat)
  rn  <- character(total_rows)
  
  # 4) fill univariate indicator rows
  r <- 1L
  for(i in seq_len(p)) {
    for(cat in 2:m[i]) {
      out[r, ] <- as.integer(patterns[[i]] == cat)
      rn[r]   <- paste0("Y", i, "=", cat)
      r       <- r + 1L
    }
  }
  
  # 5) fill bivariate indicator rows
  for(i in seq_len(p-1)) for(j in (i+1):p) {
    for(c1 in 2:m[i]) for(c2 in 2:m[j]) {
      out[r, ] <- as.integer(patterns[[i]] == c1 & patterns[[j]] == c2)
      rn[r]   <- paste0("Y", i, "=", c1, ",Y", j, "=", c2)
      r       <- r + 1L
    }
  }
  
  rownames(out) <- rn
  colnames(out) <- apply(patterns, 1, paste0, collapse = "")
  out
}
CREATE_T2_MAT(rep(2, 5))

          11111 11112 11121 11122 11211 11212 11221 11222 12111 12112 12121
Y1=2          0     0     0     0     0     0     0     0     0     0     0
Y2=2          0     0     0     0     0     0     0     0     1     1     1
Y3=2          0     0     0     0     1     1     1     1     0     0     0
Y4=2          0     0     1     1     0     0     1     1     0     0     1
Y5=2          0     1     0     1     0     1     0     1     0     1     0
Y1=2,Y2=2     0     0     0     0     0     0     0     0     0     0     0
Y1=2,Y3=2     0     0     0     0     0     0     0     0     0     0     0
Y1=2,Y4=2     0     0     0     0     0     0     0     0     0     0     0
Y1=2,Y5=2     0     0     0     0     0     0     0     0     0     0     0
Y2=2,Y3=2     0     0     0     0     0     0     0     0     0     0     0
Y2=2,Y4=2     0     0     0     0     0     0     0     0     0     0     1
Y2=2,Y5=2     0     0     0     0     0     0     0     0     0     1     0
Y3=2,Y4=2     0     0     0     0     0     0     1     1     0     0     0
Y3=2,Y5=2     0     0     0     0     0     1     0     1     0     0     0
Y4=2,Y5=2     0     0     0     1     0     0     0     1     0     0     0
          12122 12211 12212 12221 12222 21111 21112 21121 21122 21211 21212
Y1=2          0     0     0     0     0     1     1     1     1     1     1
Y2=2          1     1     1     1     1     0     0     0     0     0     0
Y3=2          0     1     1     1     1     0     0     0     0     1     1
Y4=2          1     0     0     1     1     0     0     1     1     0     0
Y5=2          1     0     1     0     1     0     1     0     1     0     1
Y1=2,Y2=2     0     0     0     0     0     0     0     0     0     0     0
Y1=2,Y3=2     0     0     0     0     0     0     0     0     0     1     1
Y1=2,Y4=2     0     0     0     0     0     0     0     1     1     0     0
Y1=2,Y5=2     0     0     0     0     0     0     1     0     1     0     1
Y2=2,Y3=2     0     1     1     1     1     0     0     0     0     0     0
Y2=2,Y4=2     1     0     0     1     1     0     0     0     0     0     0
Y2=2,Y5=2     1     0     1     0     1     0     0     0     0     0     0
Y3=2,Y4=2     0     0     0     1     1     0     0     0     0     0     0
Y3=2,Y5=2     0     0     1     0     1     0     0     0     0     0     1
Y4=2,Y5=2     1     0     0     0     1     0     0     0     1     0     0
          21221 21222 22111 22112 22121 22122 22211 22212 22221 22222
Y1=2          1     1     1     1     1     1     1     1     1     1
Y2=2          0     0     1     1     1     1     1     1     1     1
Y3=2          1     1     0     0     0     0     1     1     1     1
Y4=2          1     1     0     0     1     1     0     0     1     1
Y5=2          0     1     0     1     0     1     0     1     0     1
Y1=2,Y2=2     0     0     1     1     1     1     1     1     1     1
Y1=2,Y3=2     1     1     0     0     0     0     1     1     1     1
Y1=2,Y4=2     1     1     0     0     1     1     0     0     1     1
Y1=2,Y5=2     0     1     0     1     0     1     0     1     0     1
Y2=2,Y3=2     0     0     0     0     0     0     1     1     1     1
Y2=2,Y4=2     0     0     0     0     1     1     0     0     1     1
Y2=2,Y5=2     0     0     0     1     0     1     0     1     0     1
Y3=2,Y4=2     1     1     0     0     0     0     0     0     1     1
Y3=2,Y5=2     0     1     0     0     0     0     0     1     0     1
Y4=2,Y5=2     0     1     0     0     0     1     0     0     0     1

Influence matrix

To estimate the influence matrix, we need a couple of ingredients:

• Inverse Hessian matrix evaluated at the PML estimates
• Jacobian \(\partial \boldsymbol\pi_{\text{pair}}(\theta) / \partial\theta\) evaluated at the PML estimates
• Weight matrix \(\operatorname{diag}(\boldsymbol\pi_{\text{pair}}(\theta))^{-1}\)
• \(\boldsymbol G\) transformation matrix which brings \(\boldsymbol\pi_{\text{pair}} \mapsto \boldsymbol \pi\)

In [5]:

# Inverse Hessian
Hinv <- lavaan:::lav_model_information_observed(
  lavmodel = fit@Model,
  lavsamplestats = fit@SampleStats,
  lavdata = fit@Data,
  lavoptions = fit@Options,  
  lavcache = fit@Cache, 
  lavimplied = fit@Implied,
  inverted = TRUE
)
round(Hinv, 3)

        [,1]   [,2]   [,3]   [,4]   [,5]   [,6]   [,7]   [,8]   [,9] [,10]
 [1,]  6.729 -3.212  0.531 -0.450 -0.183  0.152 -0.015  0.001 -0.003 0.000
 [2,] -3.212  6.346 -1.783 -0.694 -0.623 -0.002  0.013  0.001  0.004 0.001
 [3,]  0.531 -1.783  3.180 -0.215  0.047  0.003  0.011 -0.006  0.001 0.000
 [4,] -0.450 -0.694 -0.215  3.169 -0.107  0.002  0.006  0.001  0.026 0.001
 [5,] -0.183 -0.623  0.047 -0.107  3.573  0.002  0.004  0.001  0.001 0.038
 [6,]  0.152 -0.002  0.003  0.002  0.002  0.844  0.037  0.019  0.022 0.016
 [7,] -0.015  0.013  0.011  0.006  0.004  0.037  0.419  0.020  0.021 0.015
 [8,]  0.001  0.001 -0.006  0.001  0.001  0.019  0.020  0.389  0.012 0.009
 [9,] -0.003  0.004  0.001  0.026  0.001  0.022  0.021  0.012  0.471 0.009
[10,]  0.000  0.001  0.000  0.001  0.038  0.016  0.015  0.009  0.009 0.590

# Jacobian -- for PML, there are 4 x (5C2) = 40 rows corresponding to pairwise
# probabilities.
Delta <- lavaan.bingof:::get_Delta_mats(fit)$Delta_til
round(Delta, 3)

        [,1]   [,2]   [,3]   [,4]   [,5]   [,6]   [,7]   [,8]   [,9]  [,10]
 [1,]  0.045  0.043  0.000  0.000  0.000  0.085  0.030  0.000  0.000  0.000
 [2,] -0.045 -0.043  0.000  0.000  0.000 -0.085  0.323  0.000  0.000  0.000
 [3,] -0.045 -0.043  0.000  0.000  0.000  0.058 -0.030  0.000  0.000  0.000
 [4,]  0.045  0.043  0.000  0.000  0.000 -0.058 -0.323  0.000  0.000  0.000
 [5,]  0.023  0.000  0.038  0.000  0.000  0.092  0.000  0.028  0.000  0.000
 [6,] -0.023  0.000 -0.038  0.000  0.000 -0.092  0.000  0.371  0.000  0.000
 [7,] -0.023  0.000 -0.038  0.000  0.000  0.051  0.000 -0.028  0.000  0.000
 [8,]  0.023  0.000  0.038  0.000  0.000 -0.051  0.000 -0.371  0.000  0.000
 [9,]  0.023  0.000  0.000  0.038  0.000  0.053  0.000  0.000  0.031  0.000
[10,] -0.023  0.000  0.000 -0.038  0.000 -0.053  0.000  0.000  0.277  0.000
[11,] -0.023  0.000  0.000 -0.038  0.000  0.090  0.000  0.000 -0.031  0.000
[12,]  0.023  0.000  0.000  0.038  0.000 -0.090  0.000  0.000 -0.277  0.000
[13,]  0.013  0.000  0.000  0.000  0.029  0.031  0.000  0.000  0.000  0.024
[14,] -0.013  0.000  0.000  0.000 -0.029 -0.031  0.000  0.000  0.000  0.206
[15,] -0.013  0.000  0.000  0.000 -0.029  0.112  0.000  0.000  0.000 -0.024
[16,]  0.013  0.000  0.000  0.000  0.029 -0.112  0.000  0.000  0.000 -0.206
[17,]  0.000  0.060  0.105  0.000  0.000  0.000  0.192  0.123  0.000  0.000
[18,]  0.000 -0.060 -0.105  0.000  0.000  0.000 -0.192  0.275  0.000  0.000
[19,]  0.000 -0.060 -0.105  0.000  0.000  0.000  0.162 -0.123  0.000  0.000
[20,]  0.000  0.060  0.105  0.000  0.000  0.000 -0.162 -0.275  0.000  0.000
[21,]  0.000  0.050  0.000  0.088  0.000  0.000  0.096  0.000  0.118  0.000
[22,]  0.000 -0.050  0.000 -0.088  0.000  0.000 -0.096  0.000  0.189  0.000
[23,]  0.000 -0.050  0.000 -0.088  0.000  0.000  0.257  0.000 -0.118  0.000
[24,]  0.000  0.050  0.000  0.088  0.000  0.000 -0.257  0.000 -0.189  0.000
[25,]  0.000  0.026  0.000  0.000  0.065  0.000  0.059  0.000  0.000  0.090
[26,]  0.000 -0.026  0.000  0.000 -0.065  0.000 -0.059  0.000  0.000  0.140
[27,]  0.000 -0.026  0.000  0.000 -0.065  0.000  0.295  0.000  0.000 -0.090
[28,]  0.000  0.026  0.000  0.000  0.065  0.000 -0.295  0.000  0.000 -0.140
[29,]  0.000  0.000  0.050  0.051  0.000  0.000  0.000  0.093  0.163  0.000
[30,]  0.000  0.000 -0.050 -0.051  0.000  0.000  0.000 -0.093  0.144  0.000
[31,]  0.000  0.000 -0.050 -0.051  0.000  0.000  0.000  0.305 -0.163  0.000
[32,]  0.000  0.000  0.050  0.051  0.000  0.000  0.000 -0.305 -0.144  0.000
[33,]  0.000  0.000  0.027  0.000  0.038  0.000  0.000  0.058  0.000  0.122
[34,]  0.000  0.000 -0.027  0.000 -0.038  0.000  0.000 -0.058  0.000  0.108
[35,]  0.000  0.000 -0.027  0.000 -0.038  0.000  0.000  0.340  0.000 -0.122
[36,]  0.000  0.000  0.027  0.000  0.038  0.000  0.000 -0.340  0.000 -0.108
[37,]  0.000  0.000  0.000  0.022  0.031  0.000  0.000  0.000  0.051  0.063
[38,]  0.000  0.000  0.000 -0.022 -0.031  0.000  0.000  0.000 -0.051  0.167
[39,]  0.000  0.000  0.000 -0.022 -0.031  0.000  0.000  0.000  0.256 -0.063
[40,]  0.000  0.000  0.000  0.022  0.031  0.000  0.000  0.000 -0.256 -0.167

# Weight matrix
W <- diag(1 / unlist(lavaan:::lav_tables_pairwise_model_pi(fit)))
diag(W)

 [1] 19.255900  3.844648 41.558872  1.506242 19.042163  2.328187 42.590628
 [8]  2.022298 31.524499  4.919761 22.587116  1.387456 53.508654  7.793943
[15] 17.450234  1.256754  5.193494  3.454408  8.369227  2.509531  9.358707
[22]  7.804519  4.873732  1.786240 15.681207 12.015948  4.027981  1.653594
[29]  7.470943  9.888131  2.872062  2.399032 12.213884 15.356433  2.499002
[36]  2.208252 23.097292  9.643368  5.216807  1.512131

# Transformation matrix -- in Jamil et al. (2025), this is the design matrix
# called B such that G = B %*% T2
B  <- lavaan.bingof:::Beta_mat_design(nvar = 5)
T2 <- lavaan.bingof:::create_T2_mat(p = 5)
# G <- B %*% T2
# Matrix::Matrix(G, sparse = TRUE)
G2 <- B
Matrix::Matrix(G2, sparse = TRUE)

40 x 15 sparse Matrix of class "dgCMatrix"
                                                  
 [1,] -1 -1  .  .  .  1  .  .  .  .  .  .  .  .  .
 [2,]  1  .  .  .  . -1  .  .  .  .  .  .  .  .  .
 [3,]  .  1  .  .  . -1  .  .  .  .  .  .  .  .  .
 [4,]  .  .  .  .  .  1  .  .  .  .  .  .  .  .  .
 [5,] -1  . -1  .  .  .  1  .  .  .  .  .  .  .  .
 [6,]  1  .  .  .  .  . -1  .  .  .  .  .  .  .  .
 [7,]  .  .  1  .  .  . -1  .  .  .  .  .  .  .  .
 [8,]  .  .  .  .  .  .  1  .  .  .  .  .  .  .  .
 [9,] -1  .  . -1  .  .  .  1  .  .  .  .  .  .  .
[10,]  1  .  .  .  .  .  . -1  .  .  .  .  .  .  .
[11,]  .  .  .  1  .  .  . -1  .  .  .  .  .  .  .
[12,]  .  .  .  .  .  .  .  1  .  .  .  .  .  .  .
[13,] -1  .  .  . -1  .  .  .  1  .  .  .  .  .  .
[14,]  1  .  .  .  .  .  .  . -1  .  .  .  .  .  .
[15,]  .  .  .  .  1  .  .  . -1  .  .  .  .  .  .
[16,]  .  .  .  .  .  .  .  .  1  .  .  .  .  .  .
[17,]  . -1 -1  .  .  .  .  .  .  1  .  .  .  .  .
[18,]  .  1  .  .  .  .  .  .  . -1  .  .  .  .  .
[19,]  .  .  1  .  .  .  .  .  . -1  .  .  .  .  .
[20,]  .  .  .  .  .  .  .  .  .  1  .  .  .  .  .
[21,]  . -1  . -1  .  .  .  .  .  .  1  .  .  .  .
[22,]  .  1  .  .  .  .  .  .  .  . -1  .  .  .  .
[23,]  .  .  .  1  .  .  .  .  .  . -1  .  .  .  .
[24,]  .  .  .  .  .  .  .  .  .  .  1  .  .  .  .
[25,]  . -1  .  . -1  .  .  .  .  .  .  1  .  .  .
[26,]  .  1  .  .  .  .  .  .  .  .  . -1  .  .  .
[27,]  .  .  .  .  1  .  .  .  .  .  . -1  .  .  .
[28,]  .  .  .  .  .  .  .  .  .  .  .  1  .  .  .
[29,]  .  . -1 -1  .  .  .  .  .  .  .  .  1  .  .
[30,]  .  .  1  .  .  .  .  .  .  .  .  . -1  .  .
[31,]  .  .  .  1  .  .  .  .  .  .  .  . -1  .  .
[32,]  .  .  .  .  .  .  .  .  .  .  .  .  1  .  .
[33,]  .  . -1  . -1  .  .  .  .  .  .  .  .  1  .
[34,]  .  .  1  .  .  .  .  .  .  .  .  .  . -1  .
[35,]  .  .  .  .  1  .  .  .  .  .  .  .  . -1  .
[36,]  .  .  .  .  .  .  .  .  .  .  .  .  .  1  .
[37,]  .  .  . -1 -1  .  .  .  .  .  .  .  .  .  1
[38,]  .  .  .  1  .  .  .  .  .  .  .  .  .  . -1
[39,]  .  .  .  .  1  .  .  .  .  .  .  .  .  . -1
[40,]  .  .  .  .  .  .  .  .  .  .  .  .  .  .  1

# Influence matrix
Q <- Hinv %*% t(Delta) %*% W %*% G2
round(Q, 3)

         [,1]    [,2]    [,3]    [,4]    [,5]   [,6]   [,7]   [,8]   [,9]
 [1,] -18.554  -2.641  -9.045  -3.970  -3.316 10.969 11.410  8.188  6.278
 [2,]   7.281 -17.494  10.154   4.178   3.687  8.506 -9.280 -6.024 -4.673
 [3,]  -2.258   4.258 -16.183  -0.113  -0.892 -3.506  8.728  0.234  0.642
 [4,]  -1.940   0.112  -0.335 -13.419  -0.659 -3.342 -1.215  6.689 -0.701
 [5,]  -5.096  -2.834  -3.121  -2.531 -16.861 -2.337 -0.159 -0.499  8.171
 [6,]  -6.988   0.000   0.003   0.002   0.001  0.005 -0.010 -0.003 -0.003
 [7,]   0.018  -2.838  -0.013   0.004   0.002  0.018 -0.006 -0.019 -0.015
 [8,]  -0.004  -0.001  -2.523   0.000   0.000 -0.001  0.019 -0.002 -0.001
 [9,]   0.002   0.002   0.007  -3.257   0.004 -0.007 -0.007  0.011 -0.006
[10,]  -0.003   0.002   0.005   0.003  -4.348 -0.001 -0.002 -0.002  0.007
       [,10]  [,11]  [,12]  [,13]  [,14]  [,15]
 [1,] -2.696 -4.761 -3.217  0.087  0.236 -0.626
 [2,]  3.823  6.092  4.229 -2.835 -2.308 -1.387
 [3,]  4.427 -2.572 -1.465  3.379  2.814 -0.133
 [4,] -1.262  5.808 -0.840  3.409 -0.317  2.676
 [5,] -0.639 -0.965  7.158 -0.070  4.407  4.322
 [6,]  0.001 -0.004 -0.002  0.004  0.004  0.001
 [7,] -0.008 -0.001 -0.001  0.017  0.013  0.008
 [8,] -0.002  0.001  0.001 -0.002 -0.001  0.001
 [9,]  0.005 -0.002  0.004 -0.008  0.002 -0.002
[10,]  0.001  0.001 -0.002  0.001 -0.005 -0.002

tinytest::expect_equal(
  Q,
  lavaan.bingof:::test_begin(fit, NULL, FALSE)$B2
)

----- PASSED      : <-->
 call| tinytest::expect_equal(Q, lavaan.bingof:::test_begin(fit, NULL, 
 call| FALSE)$B2) 

\(\boldsymbol\Omega_2\) matrix

This is the (asymptotic) variance-covariance matrix of the univariate and bivariate moments.

In [6]:

Delta2 <- create_Delta2_matrix(fit)
Sigma2 <- lavaan.bingof:::create_Sigma2_matrix(fit)
D2Q <- Delta2 %*% Q

Omega2 <- 
  Sigma2 -
  D2Q %*% Sigma2 -
  Sigma2 %*% t(D2Q) +
  D2Q %*% Sigma2 %*% t(D2Q)

Matrix::Matrix(Omega2) |> 
  round(3)

15 x 15 Matrix of class "dgeMatrix"
      [,1] [,2] [,3] [,4] [,5]   [,6]   [,7]   [,8]   [,9]  [,10]  [,11]  [,12]
 [1,]    0    0    0    0    0  0.000  0.000  0.000  0.000  0.000  0.000  0.000
 [2,]    0    0    0    0    0  0.000  0.000  0.000  0.000  0.000  0.000  0.000
 [3,]    0    0    0    0    0  0.000  0.000  0.000  0.000  0.000  0.000  0.000
 [4,]    0    0    0    0    0  0.000  0.000  0.000  0.000  0.000  0.000  0.000
 [5,]    0    0    0    0    0  0.000  0.000  0.000  0.000  0.000  0.000  0.000
 [6,]    0    0    0    0    0  0.002 -0.001 -0.002 -0.001 -0.002 -0.002 -0.001
 [7,]    0    0    0    0    0 -0.001  0.006 -0.002 -0.001 -0.003  0.004  0.002
 [8,]    0    0    0    0    0 -0.002 -0.002  0.007 -0.001  0.005 -0.004  0.002
 [9,]    0    0    0    0    0 -0.001 -0.001 -0.001  0.007  0.003  0.002 -0.004
[10,]    0    0    0    0    0 -0.002 -0.003  0.005  0.003  0.009 -0.004 -0.002
[11,]    0    0    0    0    0 -0.002  0.004 -0.004  0.002 -0.004  0.010 -0.002
[12,]    0    0    0    0    0 -0.001  0.002  0.002 -0.004 -0.002 -0.002  0.010
[13,]    0    0    0    0    0  0.004 -0.004 -0.005  0.001 -0.006 -0.006  0.003
[14,]    0    0    0    0    0  0.002 -0.002  0.001 -0.003 -0.004  0.003 -0.005
[15,]    0    0    0    0    0  0.002  0.001 -0.002 -0.003  0.003 -0.003 -0.005
       [,13]  [,14]  [,15]
 [1,]  0.000  0.000  0.000
 [2,]  0.000  0.000  0.000
 [3,]  0.000  0.000  0.000
 [4,]  0.000  0.000  0.000
 [5,]  0.000  0.000  0.000
 [6,]  0.004  0.002  0.002
 [7,] -0.004 -0.002  0.001
 [8,] -0.005  0.001 -0.002
 [9,]  0.001 -0.003 -0.003
[10,] -0.006 -0.004  0.003
[11,] -0.006  0.003 -0.003
[12,]  0.003 -0.005 -0.005
[13,]  0.023 -0.003 -0.003
[14,] -0.003  0.020 -0.004
[15,] -0.003 -0.004  0.017

tinytest::expect_equal(
  Omega2,
  lavaan.bingof:::test_begin(fit, NULL, FALSE)$Omega2
)

----- PASSED      : <-->
 call| tinytest::expect_equal(Omega2, lavaan.bingof:::test_begin(fit, 
 call| NULL, FALSE)$Omega2) 

Wald and Pearson test

In [7]:

ligof_test <- function(lavobject) {
  
  n <- nobs(lavobject)
  Delta2 <- create_Delta2_matrix(lavobject)
  # Delta2 <- lavaan.bingof:::get_Delta_mats(lavobject)$Delta2
  Sigma2 <- lavaan.bingof:::create_Sigma2_matrix(lavobject, method = "theoretical")
  uni_bi_moments <- lavaan.bingof::get_uni_bi_moments(lavobject)
  p2_hat <- with(uni_bi_moments, c(pdot1, pdot2))
  pi2_hat <- with(uni_bi_moments, c(pidot1, pidot2))
  e2_hat <- p2_hat - pi2_hat

  # Build influence matrix
  Hinv <- lavaan:::lav_model_information_observed(
    lavmodel = lavobject@Model,
    lavsamplestats = lavobject@SampleStats,
    lavdata = lavobject@Data,
    lavoptions = lavobject@Options,  
    lavcache = lavobject@Cache, 
    lavimplied = lavobject@Implied,
    inverted = TRUE
  )
  Delta <- lavaan.bingof:::get_Delta_mats(lavobject)$Delta_til
  W <- diag(1 / unlist(lavaan:::lav_tables_pairwise_model_pi(lavobject)))
  G2 <- lavaan.bingof:::Beta_mat_design(nvar = 5)
  Q <- Hinv %*% t(Delta) %*% W %*% G2
  
  # Build Omega2 matrix
  D2Q <- Delta2 %*% Q
  Omega2 <- 
    Sigma2 -
    D2Q %*% Sigma2 -
    Sigma2 %*% t(D2Q) +
    D2Q %*% Sigma2 %*% t(D2Q)
  Omega2 <- (Omega2 + t(Omega2)) / 2

  out <- list()
  
  # Wald test
  Xi <- MASS::ginv(Omega2)
  X2 <- n * colSums(e2_hat * (Xi %*% e2_hat))
  df <- Matrix::rankMatrix(Omega2) - ncol(Delta2)
  pval <- pchisq(X2, df, lower.tail = FALSE)
  out$Wald <- tibble(X2 = X2, df = df, pval = pval)
  # out$WaldLB <- lavaan.bingof::Wald_test(lavobject) |> select(X2, df, pval)
  
  # Pearson test
  Xi <- diag(1 / pi2_hat)
  X2 <- n * colSums(e2_hat * (Xi %*% e2_hat))
  df <- nrow(Delta2) - ncol(Delta2)
  out$Pearson <- 
    lavaan.bingof:::moment_match(X2, Xi, Omega2, df, 3) |>
    as_tibble()
  out$Pearson$pval <- pchisq(out$Pearson$X2, df, lower.tail = FALSE)
  # out$PearsonLB <- lavaan.bingof::Pearson_test(lavobject) |> select(X2, df, pval)

  out
}

ligof_test(fit)

$Wald
# A tibble: 1 × 3
     X2    df  pval
  <dbl> <int> <dbl>
1  3.51     5 0.621

$Pearson
# A tibble: 1 × 3
     X2    df  pval
  <dbl> <dbl> <dbl>
1  2.23  3.41 0.817

Verification

In [8]:

library(furrr)

Loading required package: future

plan(multisession)
B <- 2000  # no. of simulations

sim_fun <- function(i) {
  set.seed(i)
  dat <- simulate_data(n = 1000)
  fit <- lavaan::cfa("f1 =~ y1 + y2 + y3 + y4 + y5", dat, std.lv = TRUE, estimator = "PML")
  ligof_test(fit) |>
    bind_rows(.id = "name") |>
    mutate(sim = i, name = factor(name, levels = c("Wald", "Pearson"))) |>
    select(sim, everything())
}

res <- future_map(seq_len(B), sim_fun, .progress = TRUE,
                  .options = furrr_options(seed = TRUE))

Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative
Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative
Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative
Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative
Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative
Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative
Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative
Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative
Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative
Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative
Warning: lavaan->lav_object_post_check():  
   some estimated ov variances are negative

In [9]:

bind_rows(res) |>
  mutate(
    df = mean(df),
    observed = sort(X2),
    expected = qchisq(ppoints(n()), df = df),
    .by = name
  ) |>
  ggplot(aes(expected, observed, col = name)) +
  geom_point() +
  geom_abline(slope = 1, intercept = 0, linetype = "dashed") +
  labs(
    title = "QQ-plot of M2 against chi-square distribution with 5 df",
    x = "Theoretical quantiles",
    y = "Sample quantiles"
  ) +
  coord_cartesian(xlim = c(0, 20), ylim = c(0, 20)) +
  theme_bw()

In [10]:

bind_rows(res) |>
  ggplot(aes(x = X2, y = ..density.., fill = name)) +
  geom_histogram(col = "gray90") +
  geom_line(
    data = 
      bind_rows(res) |>
      group_by(name) |>
      summarise(df = mean(df), .groups = "keep") |>
      mutate(
        x = list(seq(0, 20, 0.1)),
        y = map(x, \(x) dchisq(x, df = first(df))),
        .groups = "drop"
      ) |>
      unnest(c(x, y)),
    aes(x, y),
    linewidth = 1
  ) +
  facet_wrap(name ~ ., scales = "free_y") + 
  labs(fill = NULL) +
  theme_bw()

Warning: The dot-dot notation (`..density..`) was deprecated in ggplot2 3.4.0.
ℹ Please use `after_stat(density)` instead.

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

In [11]:

bind_rows(res) |>
  ggplot(aes(x = pval, y = ..density.., fill = name)) +
  geom_histogram(binwidth = 0.05, boundary = 0, col = "white") +
  geom_hline(yintercept = 1, linetype = "dashed") +
  facet_wrap(name ~ ., scales = "free_y") + 
  labs(fill = NULL) +
  theme_bw()