Weighted pairwise likelihood and limited information goodness-of-fit tests for binary factor models

Adolphe Quetelet Seminar Series, Ghent University

Haziq Jamil

Assistant Professor in Statistics, Universiti Brunei Darussalam
Visiting Fellow, London School of Economics and Political Science

https://haziqj.ml/pligof-gent/

April 15, 2024

Irini Moustaki
London School of Economics and Political Science

Chris Skinner (1954-2020)
London School of Economics and Political Science

H Jamil, I Moustaki, C Skinner. 2023+. Pairwise likelihood estimation and limited information goodness-of-fit test statistics for binary factor analysis models under complex survey sampling. Manuscript under revision.

Introduction

Introduction

Context

Employ latent variable models (factor models) to analyse binary data \(y_1,\dots,y_p\) collected via simple random or complex sampling.

(Psychometrics)
Behavioural checklist

(Education)
Achievement test

(Sociology)
Intergenerational support

Photo credits: Unsplash @glenncarstenspeters, @ivalex, @oanhmj

Introduction (cont.)

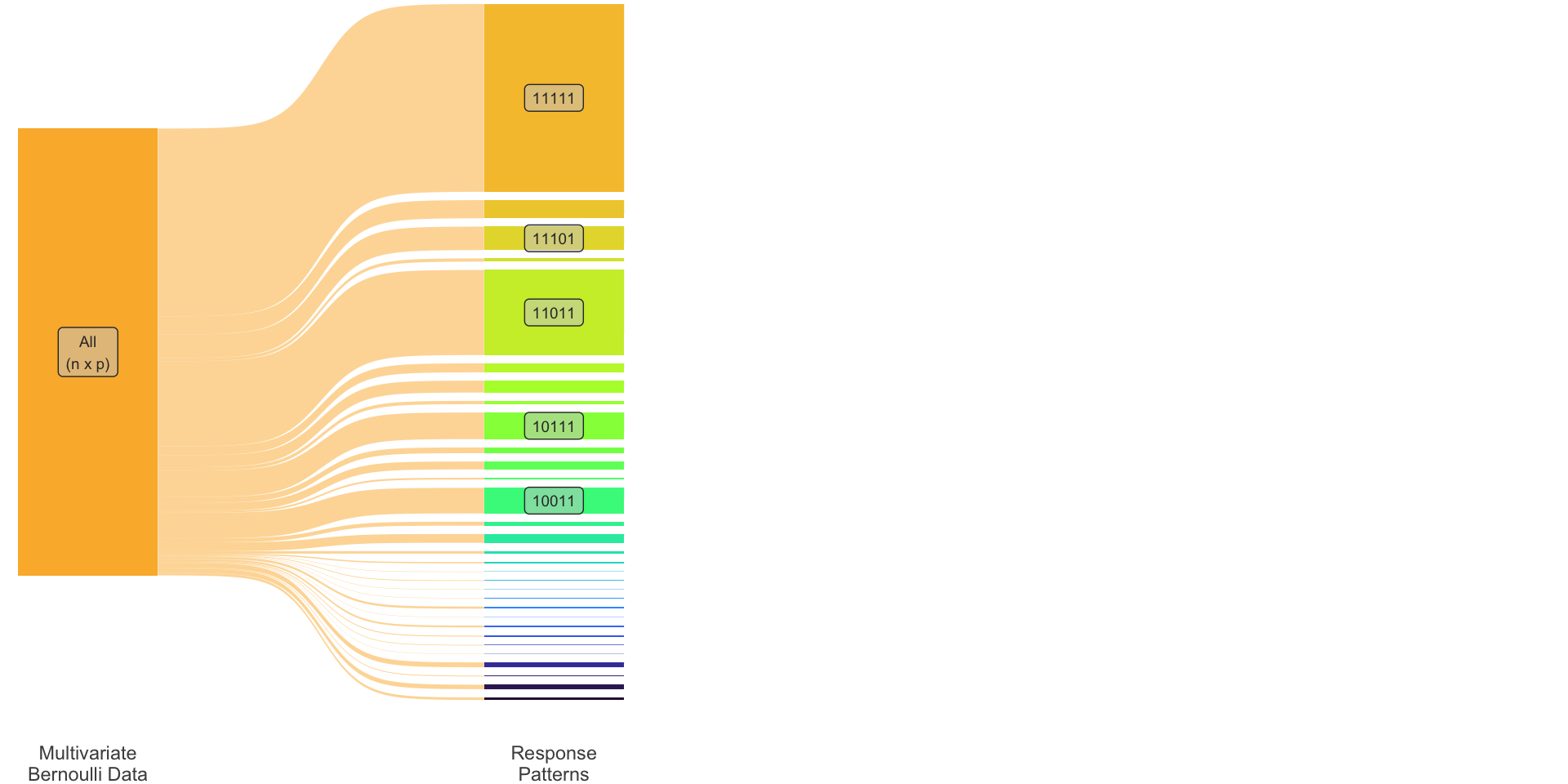
\(i\)	\(y_1\)	\(y_2\)	\(y_3\)	\(y_4\)	\(y_5\)
1	1	0	0	1	1
2	1	1	1	1	1
3	1	1	1	0	1
\(\vdots\)			\(\vdots\)
\(n\)	1	0	0	1	1

\(i\)	\(y_1\)	\(y_2\)	\(y_3\)	\(y_4\)	\(y_5\)	Pattern
1	1	0	0	1	1	10011
2	1	1	1	1	1	11111
3	1	1	1	0	1	11101
\(\vdots\)			\(\vdots\)			\(\vdots\)
\(n\)	1	0	0	1	1	10011

\(r\)	\(y_1\)	\(y_2\)	\(y_3\)	\(y_4\)	\(y_5\)	Pattern	Obs. freq
1	1	1	1	1	1	11111	343
2	1	1	0	1	1	11011	153
3	1	0	1	1	1	10111	71
\(\vdots\)			\(\vdots\)			\(\vdots\)	\(\vdots\)
\(R\)	0	1	1	1	0	01110	1

\(R = 2^p\)

\(r\)	Pattern	Obs. freq
1	11111	343
2	11011	153
3	10111	71
\(\vdots\)	\(\vdots\)	\(\vdots\)
32	01110	1

\(r\)	Pattern	Obs. freq	Exp. freq
1	11111	343	342.1
2	11011	153	151.3
3	10111	71	62.81
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
32	01110	1	0.948

\(r\)	Pattern	Obs. freq	Exp. freq
1	11111	343	342.1
2	11011	153	151.3
3	10111	71	62.81
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
28	01000	1	1.831
29	01010	1	3.276
30	01100	1	0.948
31	01101	0	0.013
32	01110	0	0.009

\(r\)	Pattern	Obs. freq	Exp. freq
1	11111	343	342.1
2	11011	153	151.3
3	10111	71	62.81
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
28	01000	1	1.831
29	01010	1	3.276
30	01100	1	0.948
31	01101	0	0.013
32	01110	0	0.009

\(r\)	Pattern	Obs. freq	Exp. freq
1	11111	360.9	342.1
2	11011	181.2	151.3
3	10111	68.05	62.81
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
28	01000	1.716	1.831
29	01010	1.120	3.276
30	01100	0.591	0.948
31	01101	0	0.013
32	01110	0	0.009

• Sparsity affects reliability of goodness-of-fit tests.
  • Limited information tests (Reiser 1996; Bartholomew and Leung 2002; Maydeu-Olivares and Joe 2005)

• Computational burden of likelihood-based models.
  • Pairwise likelihood (Varin, Reid, and Firth 2011; Katsikatsou et al. 2012)

• Unequal probability sampling (e.g. due to a complex design)
  • Incorporate design weights (Skinner 1989; Muthén and Satorra 1995)

Definitions

• Let \({\mathbf y}= (y_1, \ldots, y_p)^\top \in\{0,1\}^p\) be a vector of Bernoulli random variables.

• The joint probability of observing a response pattern \({\mathbf c}_r=(c_{r1},\dots,c_{rp})^\top\), for each \(r=1,\dots,R:=2^p\), is given by \[ \pi_r = \operatorname{P}({\mathbf y}= {\mathbf c}_r) = \operatorname{P}(y_1=c_{r1},\dots,y_p=c_{rp}), \tag{1}\] with \(\sum_{r=1}^R \pi_r = 1\).

• Suppose observations \({\mathcal Y}:= \big\{{\mathbf y}^{(h)}\big\}_{h=1}^n\) are obtained, where each unit \(h\) has a probability of selection \(1/w_h\).

• Out of convenience, sampling weights are (typically) normalised so that \(\sum_{h=1}^n w_h = n\).

  • Simple random sampling (SRS): \(w_h=1, \forall h\).
  • Stratified sampling: \(w_h = N_s(h)/N\), the stratum fractions.
  • Etc.

Multinomial distribution

• Let \(p_r = \hat n_r \big/ \sum_h w_h\) be the the \(r\)th entry of the \(R\)-vector of proportions \({\mathbf p}\), with \(\hspace{1.4cm}\)

\[ \hat n_r = \sum_{h=1}^n w_h [{\mathbf y}^{(h)} = {\mathbf c}_r]. \tag{2}\]

• The random vector \(\hat{\mathbf n}= (\hat n_1,\dots,\hat n_R)^\top\) follows a multinomial distribution with parameters \(n\), \(R\), and \({\boldsymbol\pi}:=(\pi_1,\dots,\pi_R)^\top\), with

\[ \mathop{\mathrm{E}}(\hat{\mathbf n}) = n{\boldsymbol\pi}\hspace{2em}\text{and}\hspace{2em} \mathop{\mathrm{Var}}(\hat{\mathbf n}) = n\big( \ {\color{lightgray}\overbrace{\color{black}\mathop{\mathrm{diag}}({\boldsymbol\pi}) - {\boldsymbol\pi}{\boldsymbol\pi}^\top}^{{\boldsymbol\Sigma}}} \ \big). \]

• It is widely known that (Agresti 2012) for IID samples that \[ \sqrt n ({\mathbf p}- {\boldsymbol\pi}) \xrightarrow{\text D} {\mathop{\mathrm{N}}}_R({\mathbf 0}, {\boldsymbol\Sigma}) \tag{3}\] as \(n\to\infty\). This also works for complex sampling (Fuller 2009), but \({\boldsymbol\Sigma}\) need not take a multinomial form.

Parametric models

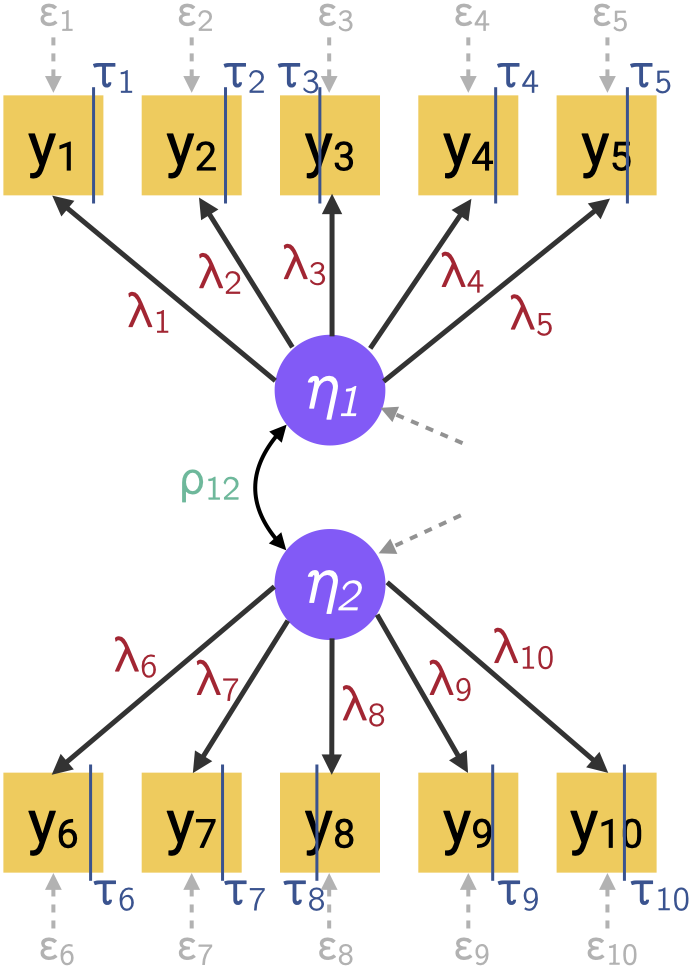
• E.g. binary factor model with underlying variable approach (s.t. constraints) \[ \begin{gathered} y_i = \begin{cases} 1 & y_i^* > \tau_i \\ 0 & y_i^* \leq \tau_i \end{cases} \\ {\mathbf y}^* = {\boldsymbol\Lambda}{\boldsymbol\eta}+ {\boldsymbol\epsilon}\\ {\boldsymbol\eta}\sim {\mathop{\mathrm{N}}}_q({\mathbf 0}, {\boldsymbol\Psi}), \hspace{3pt} {\boldsymbol\epsilon}\sim {\mathop{\mathrm{N}}}_p({\mathbf 0}, {\boldsymbol\Theta}_{\epsilon}) \end{gathered} \tag{4}\]

• The log-likelihood for \({\boldsymbol\theta}^\top = (\)\({\boldsymbol\lambda}\)\(,\,\)\({\boldsymbol\rho}\)\(,\,\)\({\boldsymbol\tau}\)\()\in\mathbb{R}^m\) is \[ \log L({\boldsymbol\theta}\mid {\mathcal Y}) = \sum_{r=1}^R \hat n_r \log \pi_r({\boldsymbol\theta}) \tag{5}\] where \(\pi_r({\boldsymbol\theta}) = \int \phi_p({\mathbf y}^* \mid {\mathbf 0}, {\boldsymbol\Lambda}{\boldsymbol\Psi}{\boldsymbol\Lambda}^\top + {\boldsymbol\Theta}_\epsilon) \mathop{\mathrm{d}}\hspace{0.5pt}\!{\mathbf y}^*\).

• FIML may be difficult (high-dimensional integral; perfect separation).

Composite likelihood

• Terminology: Pseudo-likelihood, quasi-likelihood (à la Wedderburn (1974) or misspecified models), limited information methods.

• Let \(\{{\mathcal A}_1,\dots,{\mathcal A}_K\}\) be a set of marginal or conditional events (partitioning the variable space). The composite likelihood is defined as (Lindsay 1988) \[ {\mathcal L}({\boldsymbol\theta}\mid {\mathbf y}) = \prod_{k=1}^K L({\boldsymbol\theta}\mid {\mathbf y}\in {\mathcal A}_k)^{\textcolor{lightgray}{\omega_k}} \]

• Component likelihoods \(L({\boldsymbol\theta}\mid {\mathbf y}\in {\mathcal A}_k)\) are either conditional (Besag 1974; Liang 1987; Molenberghs and Verbeke 2006) or marginal (Chandler and Bate 2007; Cox and Reid 2004; Varin 2008) densities.

• Composite likelihood enjoys nice features (Varin, Reid, and Firth 2011): relatively efficient, robust, and easier to maximise (smoother surface).

An analogy

One may enjoy the approximate picture despite
not being able to see every blade of grass.

Pairwise likelihood estimation

• For pairs of variables \(y_i\) and \(y_j\), \(i,j=1,\dots,p\), and \(i<j\), define \(\hspace{5cm}\) \[ \pi_{cc'}^{(ij)}({\boldsymbol\theta}) = \operatorname{P}_{{\boldsymbol\theta}}(y_i = c, y_i = c'), \hspace{2em} c,c'\in\{0,1\}. \tag{6}\] There are \(\tilde R = 4 \times \binom{p}{2}\) such probabilities, with \(\sum_{c,c'} \pi_{cc'}^{(ij)}({\boldsymbol\theta}) = 1\).

• The pairwise log-likelihood takes the form (Katsikatsou et al. 2012) \[ \log \operatorname{\mathcal L_{\text P}}({\boldsymbol\theta}\mid {\mathcal Y}) = \sum_{i<j} \sum_{c}\sum_{c'} \hat n_{cc'}^{(ij)} \log \pi_{y_iy_j}^{(ij)}({\boldsymbol\theta}), \tag{7}\] where \(\hat n_{cc'}^{(ij)} = \sum_h w_h [{\mathbf y}^{(h)}_i = c, {\mathbf y}^{(h)}_j = c']\).

• The evaluation of Equation 7 now involves only bivariate normal integrals! \[ \pi_{cc'}^{(ij)}({\boldsymbol\theta}) = \iint \phi_2\big({\mathbf y}^*_{ij} \mid {\mathbf 0}, {\boldsymbol\Sigma}_{y^*}^{(ij)} ({\boldsymbol\theta})\big) \mathop{\mathrm{d}}\hspace{0.5pt}\!{\mathbf y}^*_{ij} \]

MPLE properties

• Let \(\hat{\boldsymbol\theta}_{\text{PL}}= \mathop{\mathrm{argmax}}_{{\boldsymbol\theta}} \operatorname{\mathcal L_{\text P}}({\boldsymbol\theta}\mid {\mathcal Y})\). Under certain regularity conditions (Varin, Reid, and Firth 2011), as \(n\to\infty\), \[ \sqrt n (\hat{\boldsymbol\theta}_{\text{PL}}- {\boldsymbol\theta}) \xrightarrow{\text D} {\mathop{\mathrm{N}}}_m \left( {\mathbf 0}, \left\{ {\mathcal H}({\boldsymbol\theta}){\mathcal J}({\boldsymbol\theta})^{-1}{\mathcal H}({\boldsymbol\theta}) \right\}^{-1} \right),\hspace{1em} \text{where} \tag{8}\]
  • \({\mathcal H}({\boldsymbol\theta})=-\mathop{\mathrm{E}}\nabla^2\log \operatorname{\mathcal L_{\text P}}({\boldsymbol\theta}\mid {\mathbf y}^{(h)})\) is the sensitivity matrix; and
  • \({\mathcal J}({\boldsymbol\theta})=\mathop{\mathrm{Var}}\big(\nabla\log\operatorname{\mathcal L_{\text P}}({\boldsymbol\theta}\mid {\mathbf y}^{(h)})\big)\) is the variability matrix.

• Estimators of these matrices are given by (Zhao and Joe 2005; Asparouhov 2005)

\[ \begin{aligned} \hat{\mathbf H}&= - \frac{1}{\sum_h w_h} \sum_h \nabla^2\log \operatorname{\mathcal L_{\text P}}({\boldsymbol\theta}\mid {\mathbf y}^{(h)}) \Bigg|_{{\boldsymbol\theta}= \hat{\boldsymbol\theta}_{\text{PL}}} \hspace{2em}\text{and} \\ \hat{\mathbf J}&= \frac{1}{\sum_h w_h} \sum_h \nabla\log \operatorname{\mathcal L_{\text P}}({\boldsymbol\theta}\mid {\mathbf y}^{(h)}) \nabla\log \operatorname{\mathcal L_{\text P}}({\boldsymbol\theta}\mid {\mathbf y}^{(h)})^\top \Bigg|_{{\boldsymbol\theta}= \hat{\boldsymbol\theta}_{\text{PL}}}. \end{aligned} \tag{9}\]

Limited information GOF tests

Goodness-of-fit

• GOF tests are usually constructed by inspecting the fit of the joint probabilities \(\hat\pi_r := \pi_r(\hat{\boldsymbol\theta})\).

• Most common tests are

  • LR: \(X^2 = 2n\sum_r p_r\log( p_r/\hat\pi_r)\);
  • Pearson: \(X^2 = n\sum_r ( p_r - \hat\pi_r)^2 / \hat\pi_r\).

  These tests are asymptotically distributed as chi square.

• Likely to face sparsity issues (small or zero cell counts) which distort the approximation to the chi square.

Limited information goodness-of-fit (LIGOF)

Consider instead the fit of the lower order marginals.

• Univariate: \(\ \dot\pi_i := \operatorname{P}(y_i = 1)\)

• Bivariate: \(\ \dot\pi_{ij} := \operatorname{P}(y_i = 1, y_j=1)\)

• Collectively \[ {\boldsymbol\pi}_2 = \begin{pmatrix} \dot{\boldsymbol\pi}_1 \\ \dot{\boldsymbol\pi}_2 \\ \end{pmatrix} = \begin{pmatrix} (\dot\pi_1, \dots, \dot\pi_p)^\top \\ \big(\dot\pi_{ij}\big)_{i<j} \\ \end{pmatrix} \] This is of dimensions \[ S=p + p(p-1)/2 \ll R. \]

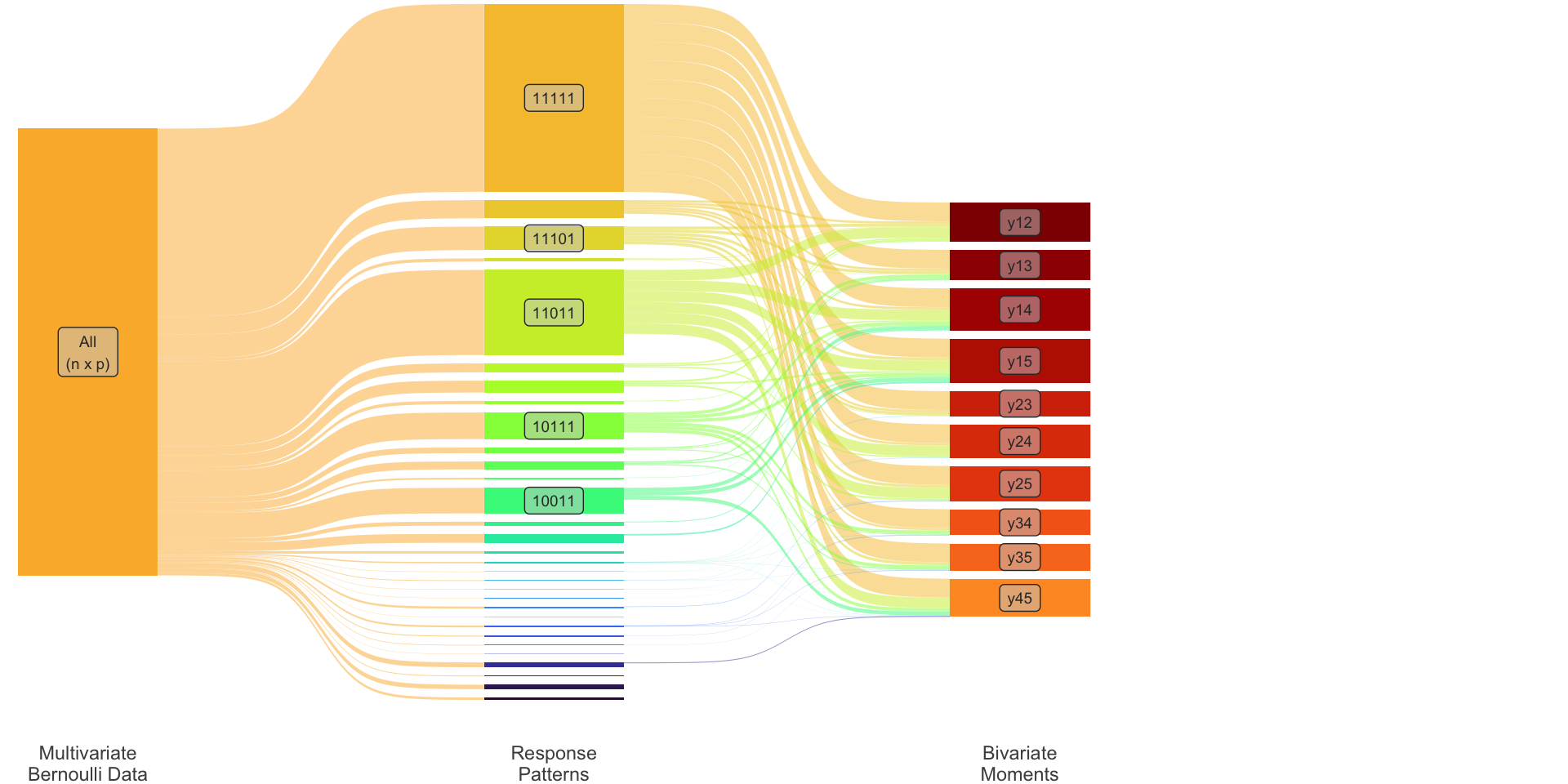
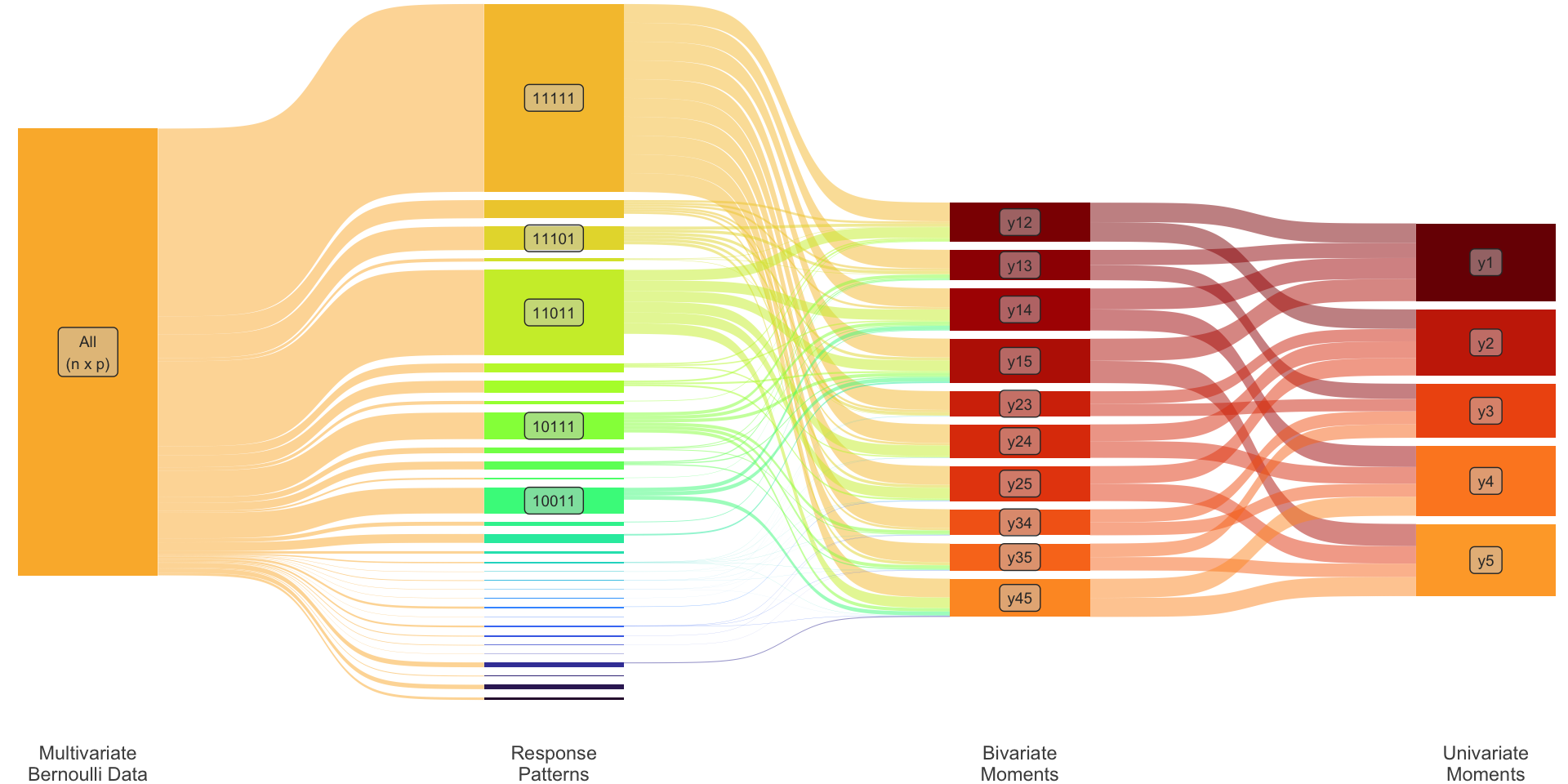
Transformation matrix

Define \({\mathbf T}_2: \mathbb{R}^R \to \mathbb{R}^S\) such that \({\boldsymbol\pi}\mapsto {\boldsymbol\pi}_2\). To illustrate, consider \(p=3\) so that \(R=2^3=8\) and \(S=3+3=6\).

\[ {\color{lightgray}\overbrace{\color{black} \left( \begin{array}{c} \dot\pi_1 \\ \dot\pi_2 \\ \dot\pi_3 \\ \hdashline \dot\pi_{12} \\ \dot\pi_{13} \\ \dot\pi_{23} \\ \end{array} \right) \vphantom{ \begin{array}{c} \pi_{000} \\ \pi_{100} \\ \pi_{010} \\ \pi_{001} \\ \pi_{110} \\ \pi_{101} \\ \pi_{011} \\ \pi_{111} \\ \end{array} } }^{{\boldsymbol\pi}_2}} = {\color{lightgray}\overbrace{\color{black} \left( \begin{array}{cccccccc} 0 & 1 & 0 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 & 1 \\ \hdashline 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ \end{array} \right) \vphantom{ \begin{array}{c} \pi_{000} \\ \pi_{100} \\ \pi_{010} \\ \pi_{001} \\ \pi_{110} \\ \pi_{101} \\ \pi_{011} \\ \pi_{111} \\ \end{array} } }^{{\mathbf T}_2}} \ {\color{lightgray}\overbrace{\color{black} \left( \begin{array}{c} \pi_{000} \\ \pi_{100} \\ \pi_{010} \\ \pi_{001} \\ \pi_{110} \\ \pi_{101} \\ \pi_{011} \\ \pi_{111} \\ \end{array} \right) }^{{\boldsymbol\pi}}} \]

See Reiser (1996) and Maydeu-Olivares and Joe (2005) for further details.

Asymptotic distribution of residuals

Theorem

Consider the lower order residuals \(\hat{\mathbf e}_2 = {\mathbf p}_2 - {\boldsymbol\pi}_2(\hat{\boldsymbol\theta}_{\text{PL}})\). Then as \(n\to\infty\), \[ \sqrt n \, \hat{\mathbf e}_2 \xrightarrow{\text D} {\mathop{\mathrm{N}}}_S\left({\mathbf 0}, {\boldsymbol\Omega}_2\right) \] where \({\boldsymbol\Omega}_2 = \left( {\mathbf I}- {\boldsymbol\Delta}_2{\mathcal H}({\boldsymbol\theta})^{-1} {\mathbf B}({\boldsymbol\theta}) \right) {\boldsymbol\Sigma}_2 \left( {\mathbf I}- {\boldsymbol\Delta}_2{\mathcal H}({\boldsymbol\theta})^{-1} {\mathbf B}({\boldsymbol\theta}) \right)^\top\),

• \({\boldsymbol\Sigma}_2 = {\mathbf T}_2{\boldsymbol\Sigma}{\mathbf T}_2^\top\) (uni & bivariate multinomial matrix);
• \({\boldsymbol\Delta}_2 = {\mathbf T}_2 \big(\partial\pi_r({\boldsymbol\theta}) / \partial\theta_k \big)_{r,k}\) (uni & bivariate derivatives);
• \({\mathcal H}({\boldsymbol\theta})\) (sensitivity matrix); and
• \({\mathbf B}({\boldsymbol\theta})\) (some transformation matrix dependent on \({\boldsymbol\theta}\)).

To use \({\boldsymbol\Omega}_2\) in practice, use “hat versions” of relevant matrices.

Distribution of test statistics

LIGOF test statistics generally take the quadratic form \[ X^2 = n \hat{\mathbf e}_2^\top \hat{\boldsymbol\Xi}\hat{\mathbf e}_2, \] where \({\boldsymbol\Xi}(\hat{\boldsymbol\theta}) =: \hat{\boldsymbol\Xi}\xrightarrow{\text P} {\boldsymbol\Xi}\) is some \(S\times S\) weight matrix. Generally, \(X^2\) is reffered to a chi square distribution under \(H_0\), because (Mathai and Provost 1992) \[ X^2 \xrightarrow{\text D} \sum_{s=1}^S \delta_s\chi^2_1 \quad \text{as} \quad n\to\infty, \] where the \(\delta_s\) are the eigenvalues of \({\mathbf M}= {\boldsymbol\Omega}_2{\boldsymbol\Xi}\). Two cases:

1. If \({\mathbf M}\) is idempotent, then the chi square is exact.
2. Otherwise, it is a sum of scaled chi squares. Can be approximated by a chi square with degrees of freedom needing estimation (Cai et al. 2006).

Test statistics used

\[\begin{gathered}X^2 = n \hat{\mathbf e}_2^\top \hat{\boldsymbol\Xi}\hat{\mathbf e}_2 \\\sqrt n \hat{\mathbf e}_2 \approx {\mathop{\mathrm{N}}}_S ({\mathbf 0}, \hat{\boldsymbol\Omega}_2)\end{gathered}\]

	Name	\(\hat{{\boldsymbol\Xi}}\)	D.f.
1	Wald	\(\hat{{\boldsymbol\Omega}}^+_2\)	\(S-m\)
2	Wald (VCF)	\({\boldsymbol\Xi}\hat{{\boldsymbol\Omega}}_2{\boldsymbol\Xi}\)	\(S-m\)
3	Wald (Diag.)	\(\mathop{\mathrm{diag}}(\hat{{\boldsymbol\Omega}}_2)^{-1}\)	est.
4	Pearson	\(\mathop{\mathrm{diag}}(\hat{{\boldsymbol\pi}}_2)^{-1}\)	est.
5	RSS	\(\mathbf I\)	est.
6	Multinomial	\(\hat{{\boldsymbol\Sigma}}_2^{-1}\)	est.

1–Reiser (1996); 2–Maydeu-Olivares and Joe (2005); 4–Bartholomew and Leung (2002);
5,6–Maydeu-Olivares and Joe (2008).

Simulation results

Factor models

• M1: 1F5V
• M2: 1F8V
• M3: 1F15V
• M4: 2F10V
• M5: 3F15V

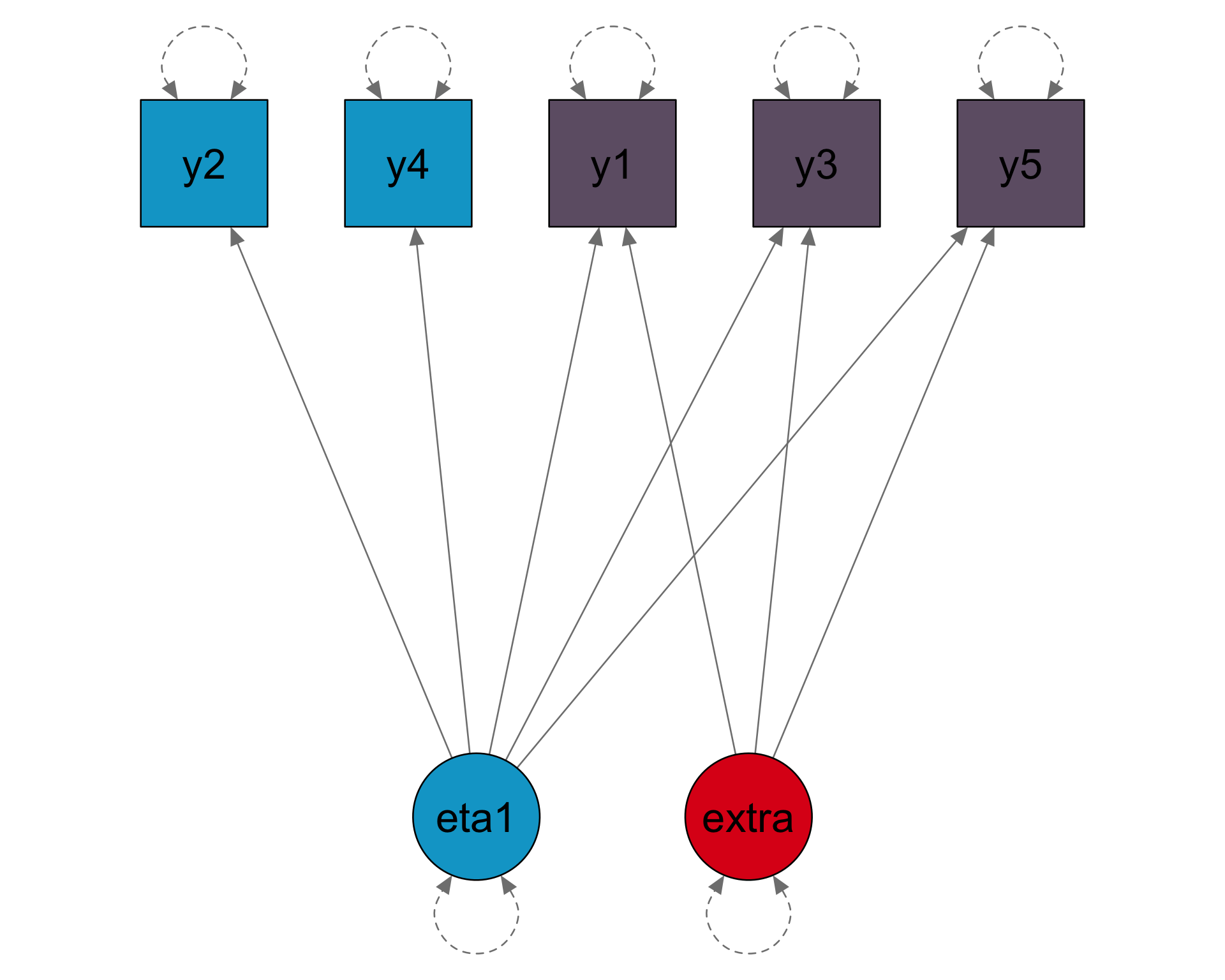
Loadings
5 x 1 sparse Matrix of class "dgCMatrix"
         
[1,] 0.80
[2,] 0.70
[3,] 0.47
[4,] 0.38
[5,] 0.34

Thresholds
[1] -1.43 -0.55 -0.13 -0.72
[5] -1.13

Factor correlations
[1] 1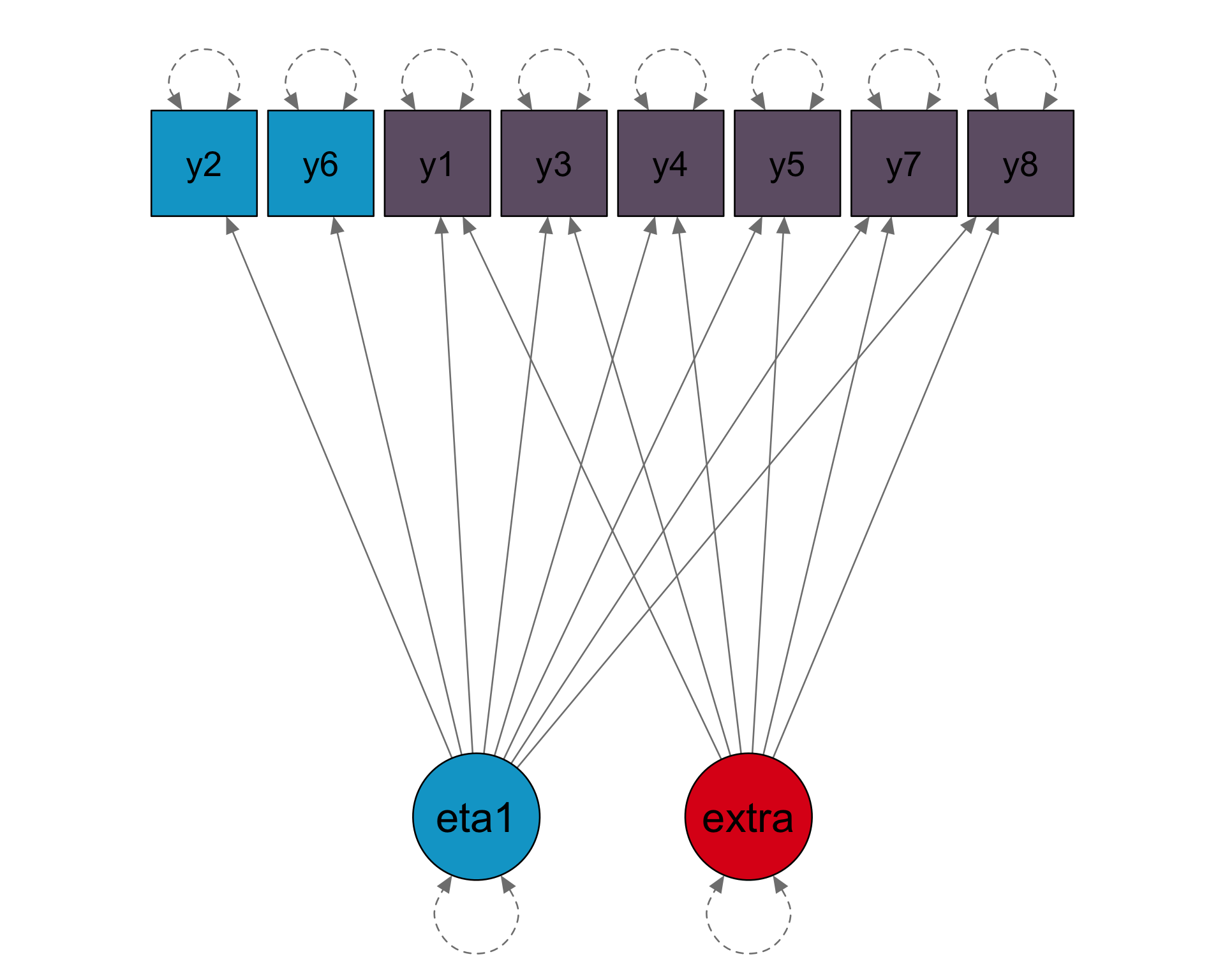

Loadings
8 x 1 sparse Matrix of class "dgCMatrix"
         
[1,] 0.80
[2,] 0.70
[3,] 0.47
[4,] 0.38
[5,] 0.34
[6,] 0.80
[7,] 0.70
[8,] 0.47

Thresholds
[1] -1.43 -0.55 -0.13 -0.72
[5] -1.13 -1.43 -0.55 -0.13

Factor correlations
[1] 1

Loadings
15 x 1 sparse Matrix of class "dgCMatrix"
          
 [1,] 0.80
 [2,] 0.70
 [3,] 0.47
 [4,] 0.38
 [5,] 0.34
 [6,] 0.80
 [7,] 0.70
 [8,] 0.47
 [9,] 0.38
[10,] 0.34
[11,] 0.80
[12,] 0.70
[13,] 0.47
[14,] 0.38
[15,] 0.34

Thresholds
 [1] -1.43 -0.55 -0.13 -0.72
 [5] -1.13 -1.43 -0.55 -0.13
 [9] -0.72 -1.13 -1.43 -0.55
[13] -0.13 -0.72 -1.13

Factor correlations
[1] 1

Loadings
10 x 2 sparse Matrix of class "dgCMatrix"
               
 [1,] 0.80 .   
 [2,] 0.70 .   
 [3,] 0.47 .   
 [4,] 0.38 .   
 [5,] 0.34 .   
 [6,] .    0.80
 [7,] .    0.70
 [8,] .    0.47
 [9,] .    0.38
[10,] .    0.34

Thresholds
 [1] -1.43 -0.55 -0.13 -0.72
 [5] -1.13 -1.43 -0.55 -0.13
 [9] -0.72 -1.13

Factor correlations
     [,1] [,2]
[1,]  1.0  0.3
[2,]  0.3  1.0

Loadings
15 x 3 sparse Matrix of class "dgCMatrix"
                    
 [1,] 0.80 .    .   
 [2,] 0.70 .    .   
 [3,] 0.47 .    .   
 [4,] 0.38 .    .   
 [5,] 0.34 .    .   
 [6,] .    0.80 .   
 [7,] .    0.70 .   
 [8,] .    0.47 .   
 [9,] .    0.38 .   
[10,] .    0.34 .   
[11,] .    .    0.80
[12,] .    .    0.70
[13,] .    .    0.47
[14,] .    .    0.38
[15,] .    .    0.34

Thresholds
 [1] -1.43 -0.55 -0.13 -0.72
 [5] -1.13 -1.43 -0.55 -0.13
 [9] -0.72 -1.13 -1.43 -0.55
[13] -0.13 -0.72 -1.13

Factor correlations
     [,1] [,2] [,3]
[1,]  1.0  0.2  0.3
[2,]  0.2  1.0  0.4
[3,]  0.3  0.4  1.0

Informative sampling

• Using M1: 1F5V, generate a fixed population size of \(N\). Then, assign each unit \(h\) a probability of selection as follows: \[ w_h^{-1} = \frac{1}{1 + \exp(y_1^*)}. \] Larger values of \(y_1^*\) result in smaller probabilities of selection.

• Sample \(n\in\{500, 1000, 5000\}\) units from a population of size \(N=n/0.01\) which ensures no need for FPC factor (Lumley 2004).

• In repeated sampling (\(B=1000\)), interested in performance of PMLE vis-à-vis

  • Bias
  • Coverage for 95% CI
  • SD/SE ratio

Informative sampling (results)

Bias

	True values	\(n = 500\)		\(n = 1000\)		\(n = 5000\)
		PML	PMLW	PML	PMLW	PML	PMLW
Loadings
\(\lambda_1\)	0.80	−0.03	0.00	−0.03	−0.01	−0.02	0.00
\(\lambda_2\)	0.70	−0.03	−0.01	−0.02	0.00	−0.03	−0.01
\(\lambda_3\)	0.47	−0.02	0.00	−0.02	0.00	−0.02	0.00
\(\lambda_4\)	0.38	−0.02	0.00	−0.02	0.00	−0.02	0.00
\(\lambda_5\)	0.34	0.00	0.01	−0.02	0.00	−0.02	−0.01
Thresholds
\(\tau_1\)	-1.43	0.31	0.00	0.31	0.00	0.30	−0.01
\(\tau_2\)	-0.55	0.22	−0.01	0.22	0.00	0.21	−0.01
\(\tau_3\)	-0.13	0.15	−0.01	0.16	0.01	0.15	0.00
\(\tau_4\)	-0.72	0.12	0.00	0.12	0.00	0.12	0.00
\(\tau_5\)	-1.13	0.11	0.01	0.11	0.01	0.11	0.00

Informative sampling (results)

Coverage and SD/SE ratio

	Coverage		SD/SE		Coverage		SD/SE		Coverage		SD/SE
	\(n = 500\)				\(n = 1000\)				\(n = 5000\)
	PML	PMLW	PML	PMLW	PML	PMLW	PML	PMLW	PML	PMLW	PML	PMLW
Loadings
\(\lambda_1\)	0.95	0.96	1.01	0.99	0.94	0.95	1.04	1.01	0.89	0.95	1.22	1.01
\(\lambda_2\)	0.95	0.95	1.03	0.99	0.93	0.95	1.09	1.01	0.85	0.95	1.31	0.99
\(\lambda_3\)	0.95	0.96	1.02	0.97	0.94	0.95	1.06	0.97	0.85	0.95	1.35	0.99
\(\lambda_4\)	0.94	0.94	1.04	1.03	0.94	0.95	1.05	1.00	0.88	0.95	1.25	1.01
\(\lambda_5\)	0.95	0.95	0.99	0.98	0.95	0.96	1.02	1.00	0.90	0.95	1.19	1.01
Thresholds
\(\tau_1\)	0.01	0.96	4.38	0.98	0.00	0.96	6.24	0.97	0.00	0.96	13.81	0.97
\(\tau_2\)	0.04	0.95	3.91	1.05	0.00	0.94	5.47	1.01	0.00	0.94	12.03	1.06
\(\tau_3\)	0.22	0.96	2.93	1.02	0.03	0.94	4.03	1.02	0.00	0.96	8.76	0.96
\(\tau_4\)	0.49	0.94	2.22	1.03	0.20	0.95	2.97	1.03	0.00	0.95	6.40	1.04
\(\tau_5\)	0.61	0.94	1.88	1.02	0.42	0.95	2.39	1.01	0.00	0.95	5.13	1.04

Educational survey

Simulate a population of \(1e6\) students clustered within classrooms and stratified by school type (correlating with abilities).

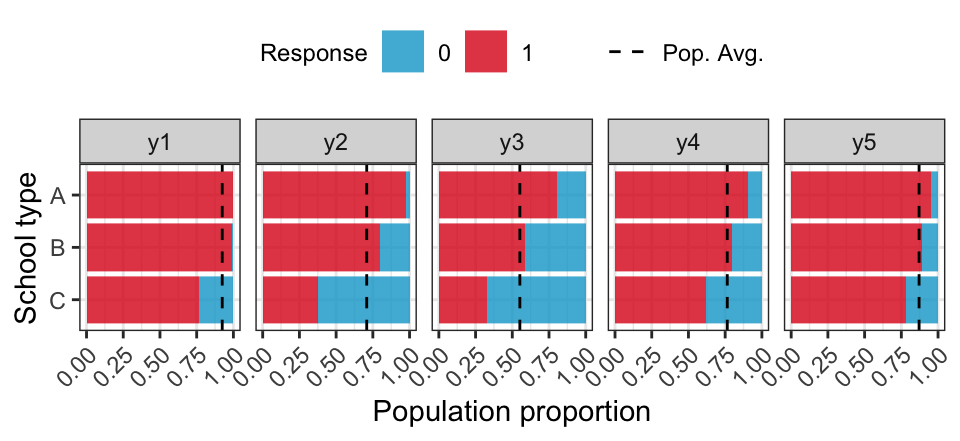
Type	\(N\)	Classes	Avg. class size
A	400	33.0	15.2
B	1000	19.6	25.6
C	600	24.9	20.4

ICC for test items range between 0.05 and 0.60.

• Cluster sample: Sample \(n_C\) schools using PPS, then sample 1 classroom via SRS, then select all students in classroom.
• Stratified cluster sample: For each stratum, sample \(n_S\) schools using SRS, then sample 1 classroom via SRS, then select all students in classroom.

Educational survey (results)

Type I error rates (5% level, \(n=5000\))

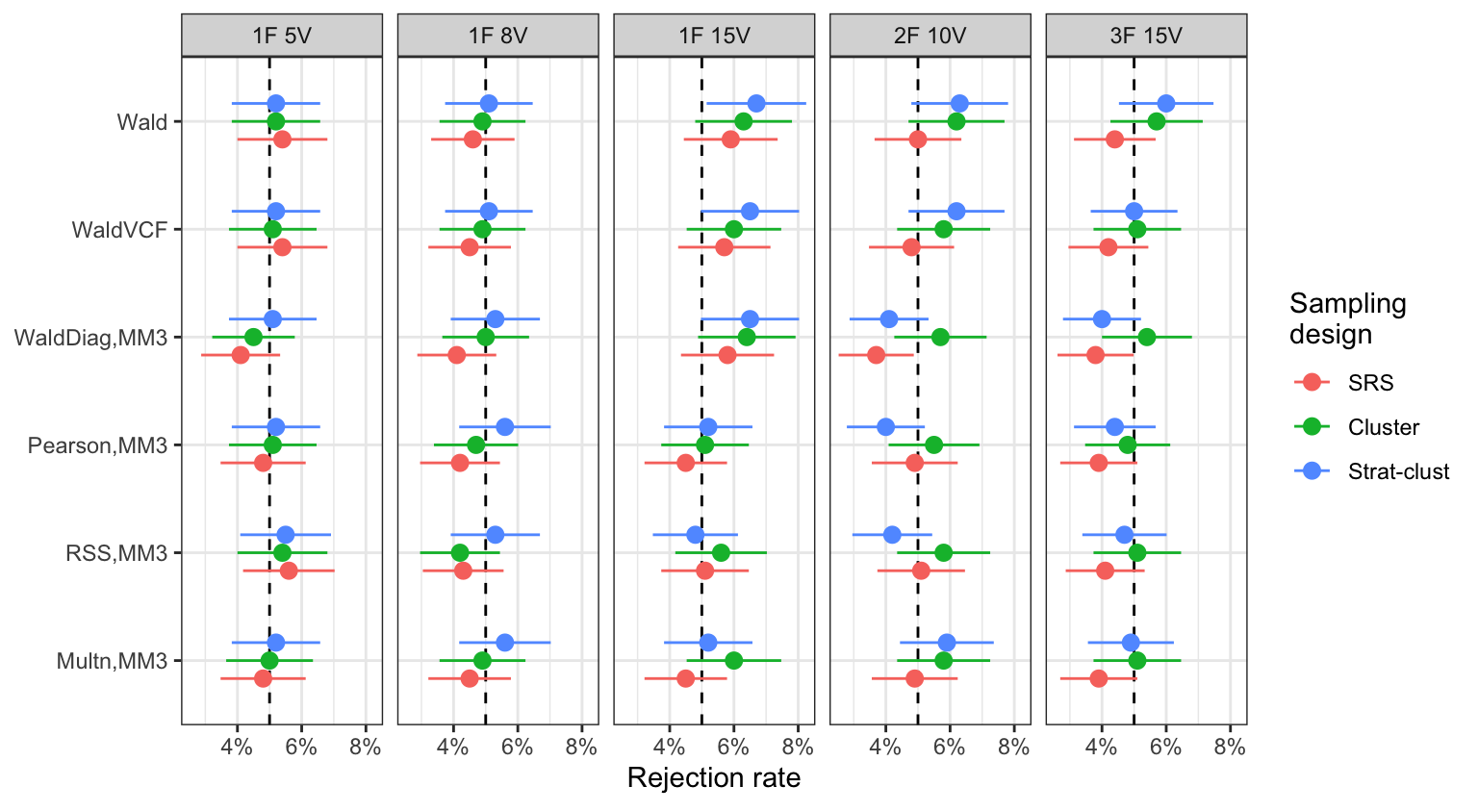
Educational survey (results)

Power analysis

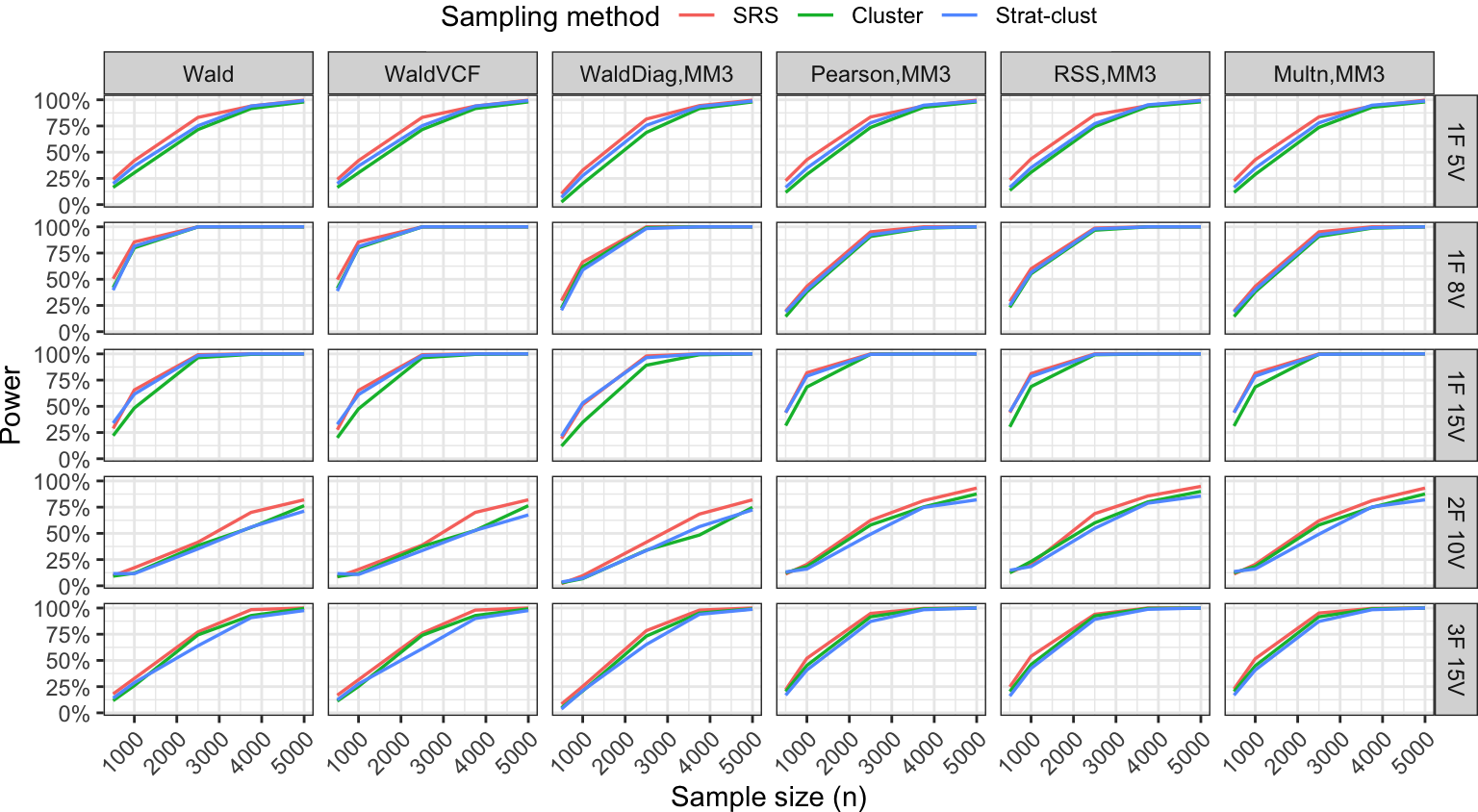
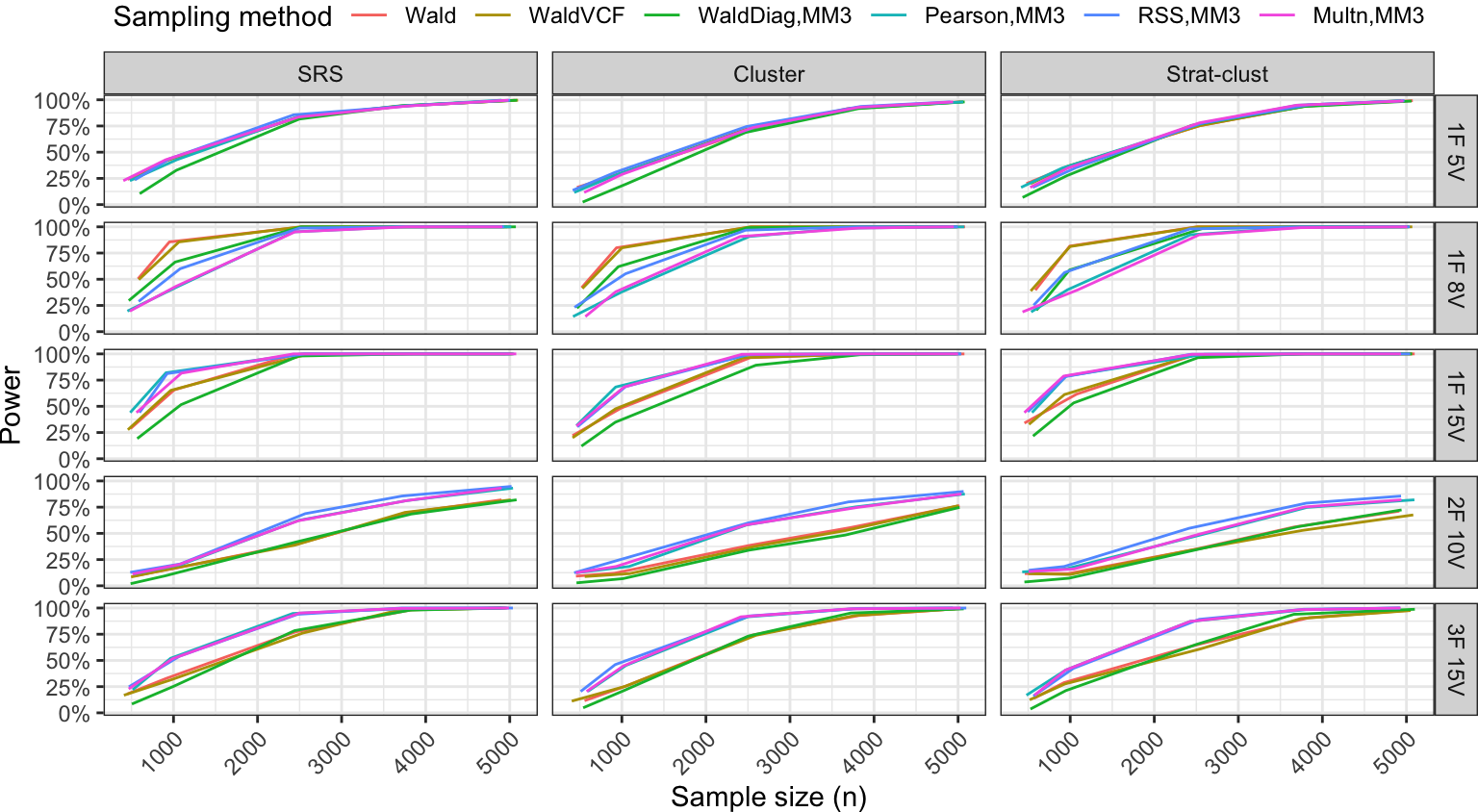
Summary

Conclusions

• Pairwise likelihood estimation alleviates some issues associated with the UV approach for binary factor models.

• Sampling weights are easily incorporated in the PML estimation, and found to perform well in (limited) simulation studies.

• Sparsity impairs the dependability of GOF tests but are circumvented by considering lower order statistics. Wald, Pearson, and others are investigated across a variety of scenarios.

  • Generally all tests have acceptable Type I errors, except WaldDiag test.
  • Wald test needs \({\boldsymbol\Omega}_2^{-1}\), but WaldVCF does not.
  • Pearson test has more power than the Wald-type test in more complicated scenarios.
  • Added variability due to complex designs (expected), but overall power curves are not drastically different.

Software

R software implementation in {lavaan} 0.6-17 (PML weights) and a separate package {lavaan.bingof} for the LIGOF tests.

fit <- lavaan::sem(
  model = "eta1 =~ y1 + y2 + y3 + y4 + y5",
  data = lavaan.bingof::gen_data_bin_wt(n = 1000),
  std.lv = TRUE,
  estimator = "PML",
  sampling.weights = "wt"
)
lavaan.bingof::all_tests(fit)

# A tibble: 6 × 6
     X2    df name          pval Xi_rank     S
  <dbl> <dbl> <chr>        <dbl>   <int> <int>
1  6.39  5    Wald         0.270      13    15
2  6.25  5    WaldVCF      0.283       5    15
3  3.65  3.29 WaldDiag,MM3 0.345      15    15
4  5.24  3.14 Pearson,MM3  0.169      15    15
5  5.86  3.82 RSS,MM3      0.191      15    15
6  5.25  3.14 Multn,MM3    0.168      15    15

https://github.com/haziqj/lavaan.bingof

Thanks!

https://haziqj.ml/plgof-gent

References

Agresti, Alan. 2012. Categorical Data Analysis. Vol. 792. John Wiley & Sons.

Asparouhov, Tihomir. 2005. “Sampling Weights in Latent Variable Modeling.” Structural Equation Modeling 12 (3): 411–34.

Bartholomew, David J, and Shing On Leung. 2002. “A Goodness of Fit Test for Sparse 2p Contingency Tables.” British Journal of Mathematical and Statistical Psychology 55 (1): 1–15.

Besag, Julian. 1974. “Spatial Interaction and the Statistical Analysis of Lattice Systems.” Journal of the Royal Statistical Society: Series B (Methodological) 36 (2): 192–225. https://doi.org/10.1111/j.2517-6161.1974.tb00999.x.

Cai, Li., Albert. Maydeu‐Olivares, Donna L. Coffman, and David. Thissen. 2006. “Limited‐information Goodness‐of‐fit Testing of Item Response Theory Models for Sparse 2 ^P Tables.” British Journal of Mathematical and Statistical Psychology 59 (1): 173–94. https://doi.org/10.1348/000711005X66419.

Chandler, Richard E., and Steven Bate. 2007. “Inference for Clustered Data Using the Independence Loglikelihood.” Biometrika 94 (1): 167–83. https://www.jstor.org/stable/20441361.

Cox, D. R., and N. Reid. 2004. “A Note on Pseudolikelihood Constructed from Marginal Densities.” Biometrika 91 (3): 729–37. https://www.jstor.org/stable/20441134.

Fuller, Wayne A. 2009. Introduction to Statistical Time Series. John Wiley & Sons.

Katsikatsou, Myrsini, Irini Moustaki, Fan Yang-Wallentin, and Karl G Jöreskog. 2012. “Pairwise Likelihood Estimation for Factor Analysis Models with Ordinal Data.” Computational Statistics & Data Analysis 56 (12): 4243–58.

Liang, Kung-Yee. 1987. “Extended Mantel-Haenszel Estimating Procedure for Multivariate Logistic Regression Models.” Biometrics 43 (2): 289–99. https://doi.org/10.2307/2531813.

Lindsay, Bruce G. 1988. “Composite Likelihood Methods.” In Contemporary Mathematics, edited by N. U. Prabhu, 80:221–39. Providence, Rhode Island: American Mathematical Society. https://doi.org/10.1090/conm/080/999014.

Lumley, Thomas. 2004. “Analysis of Complex Survey Samples.” Journal of Statistical Software 9 (April): 1–19. https://doi.org/10.18637/jss.v009.i08.

Mathai, Arakaparampil M, and Serge B Provost. 1992. Quadratic Forms in Random Variables: Theory and Applications. Dekker.

Maydeu-Olivares, Alberto, and Harry Joe. 2005. “Limited- and Full-Information Estimation and Goodness-of-Fit Testing in \(2^n\) Contingency Tables: A Unified Framework.” Journal of the American Statistical Association 100 (471): 1009–20.

———. 2008. “An Overview of Limited Information Goodness-of-Fit Testing in Multidimensional Contingency Tables.” New Trends in Psychometrics, 253–62.

Molenberghs, Geert, and Geert Verbeke. 2006. Models for Discrete Longitudinal Data. Nachdr. Springer Series in Statistics. New York, NY: Springer.

Muthén, Bengt O., and Albert Satorra. 1995. “Complex Sample Data in Structural Equation Modeling.” Sociological Methodology 25: 267–316. https://doi.org/10.2307/271070.

Reiser, Mark. 1996. “Analysis of Residuals for the Multionmial Item Response Model.” Psychometrika 61: 509–28.

Skinner, C. J. 1989. “Domain Means, Regression and Multivariate Analysis.” In Analysis of Complex Surveys, edited by C. J. Skinner, D. Holt, and T. M. F. Smith, 59–87. Wiley Series in Probability and Mathematical Statistics. Chichester; New York: Wiley.

Varin, Cristiano. 2008. “On Composite Marginal Likelihoods.” AStA Advances in Statistical Analysis 92 (1): 1–28. https://doi.org/10.1007/s10182-008-0060-7.

Varin, Cristiano, Nancy Reid, and David Firth. 2011. “An Overview of Composite Likelihood Methods.” Statistica Sinica, 5–42.

Wedderburn, R. W. M. 1974. “Quasi-Likelihood Functions, Generalized Linear Models, and the Gauss-Newton Method.” Biometrika 61 (3): 439–47. https://doi.org/10.2307/2334725.

Zhao, Y, and H. Joe. 2005. “Composite Likelihood Estimation in Multivariate Data Analysis.” Tha Canadian Journal of Statistics 33 (3): 335–56.