Plugin penalties

Haziq Jamil

Introduction

For the iRBM method, we can use an additional plugin penalty to the objective function. The plugin penalty acts to shrink the parameter estimates towards some value, thus ensuring that the estimates are finite. In some cases it might make sense to have penalties shrink to zero, but for others, this is a bit too harsh (e.g. variance parameters or other parameters which are in truth far away from zero). In these cases, it is more useful to implement a bounded penalty, where such a function acts within a pre-specified parameter range, and penalises the objective function if the parameter estimates stray to the boundaries. Yet another penalty function that will be explored is a penalty function that shrinks the estimates towards some “ideal” variance-covariance matrix.

Here are the penalty functions:

1. Ridge penalty (to target $x^*$) $$f(x) = \Vert x - x^* \Vert^2$$ Here, $x^*$ could be ideal parameter values, or could be used in conjunction with bounds where $x^*$ is the midpoint of the bounds.

2. Ridge penalty with bounds $l \leq x \leq u$ $$f(x) = \begin{cases} 0 & \text{if } l \leq x \leq u \\ \Vert x - l \Vert^2 & \text{if } x < l \\ \Vert x - u \Vert^2 & \text{if } x > u \end{cases}$$

3. Huber penalty with bounds $l \leq x \leq u$ $$f(x) = \begin{cases} \frac{1}{2} y^2 & \text{if } |y| < \tau, \\[10pt] -\tau \left(\frac{\tau}{2} - |y|\right) & \text{if } |y| \geq \tau, \end{cases}$$ where $\tau$ is some threshold (defaults to 1), and $$y = \begin{cases} \log\left(\frac{x - l}{u - x}\right) & \text{if } l,u < \infty \\ \log(x - l) & \text{if } l < \infty, u = \infty \\ 0 & \text{if } l,u = \infty \end{cases}$$

4. Matrix norm to target matrix

   To be developed!

Comparison of penalty functions

lb <- 0
ub <- 3
tibble(
  x = seq(-2, 5, length.out = 250)
) |>
  rowwise() |>
  mutate(
    ridge = brlavaan:::pen_ridge(x),
    ridge_bounded = brlavaan:::pen_ridge_bound(x, lb = lb, ub = ub),
    huber_bounded = brlavaan:::pen_huber(x, lb = lb, ub = ub),
    huber_left_bounded = brlavaan:::pen_huber(x, lb = lb, ub = Inf)
  ) |> 
  pivot_longer(-x) |>
  ggplot(aes(x, value, color = name)) +
  annotate("rect", xmin = lb, xmax = ub, ymin = -Inf, ymax = Inf, alpha = 0.2) +
  geom_line() +
  geom_vline(xintercept = c(lb, ub), linetype = "dashed") +
  labs(y = "f(x)")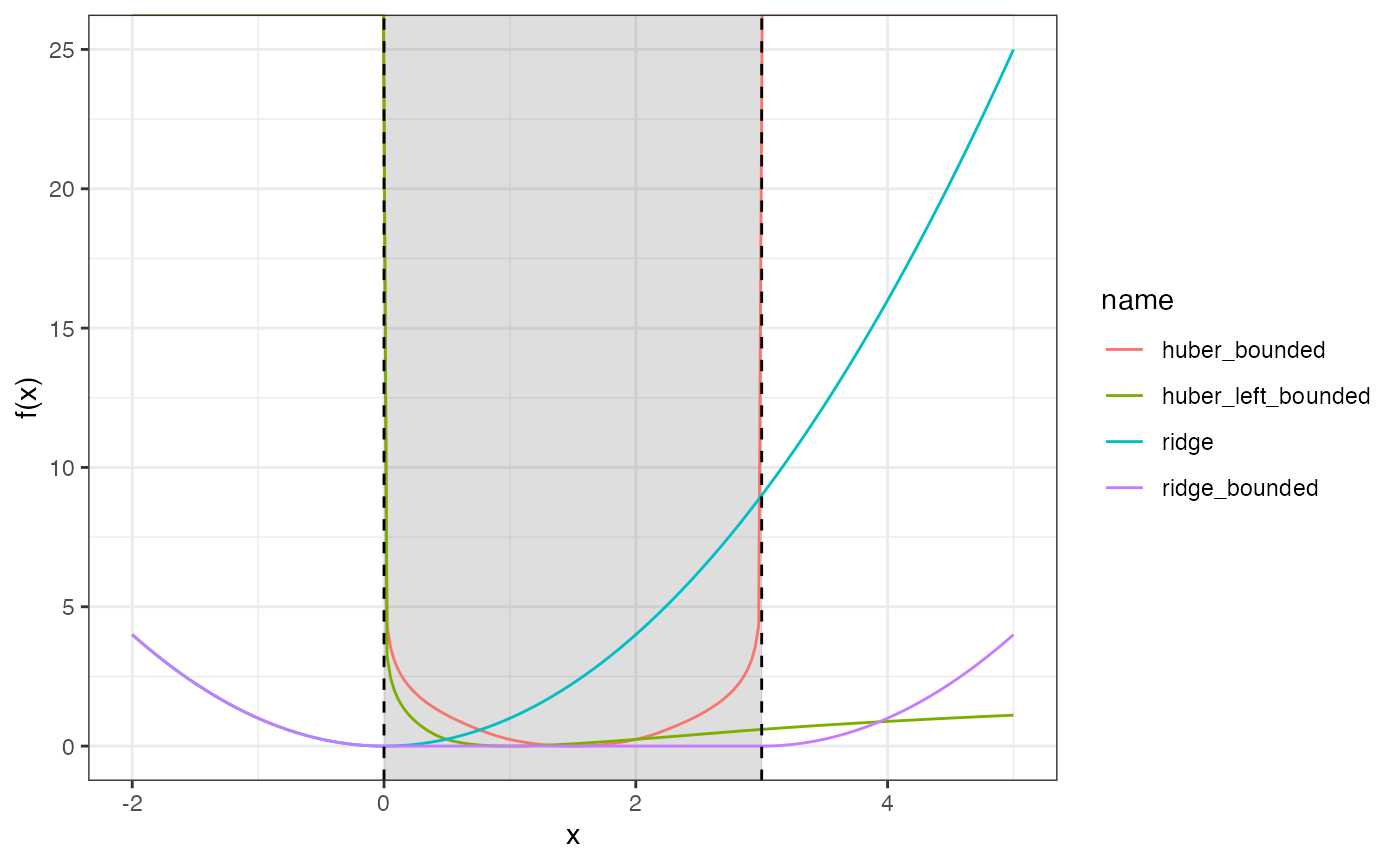

Comparison of penalty functions.

Comparing Huber penalty thresholds

lb <- -1
ub <- 4
tibble(
  x = seq(-2, 5, length.out = 250)
) |>
  rowwise() |>
  mutate(
    `0.5` = brlavaan:::pen_huber(x, lb = lb, ub = ub, thres = 0.5),
    `1` = brlavaan:::pen_huber(x, lb = lb, ub = ub, thres = 1),
    `2` = brlavaan:::pen_huber(x, lb = lb, ub = ub, thres = 2)
  ) |> 
  pivot_longer(-x) |>
  ggplot(aes(x, value, color = name)) +
  annotate("rect", xmin = lb, xmax = ub, ymin = -Inf, ymax = Inf, alpha = 0.2) +
  geom_line() +
  geom_vline(xintercept = c(lb, ub), linetype = "dashed") +
  labs(y = "f(x)", col = "Threshold")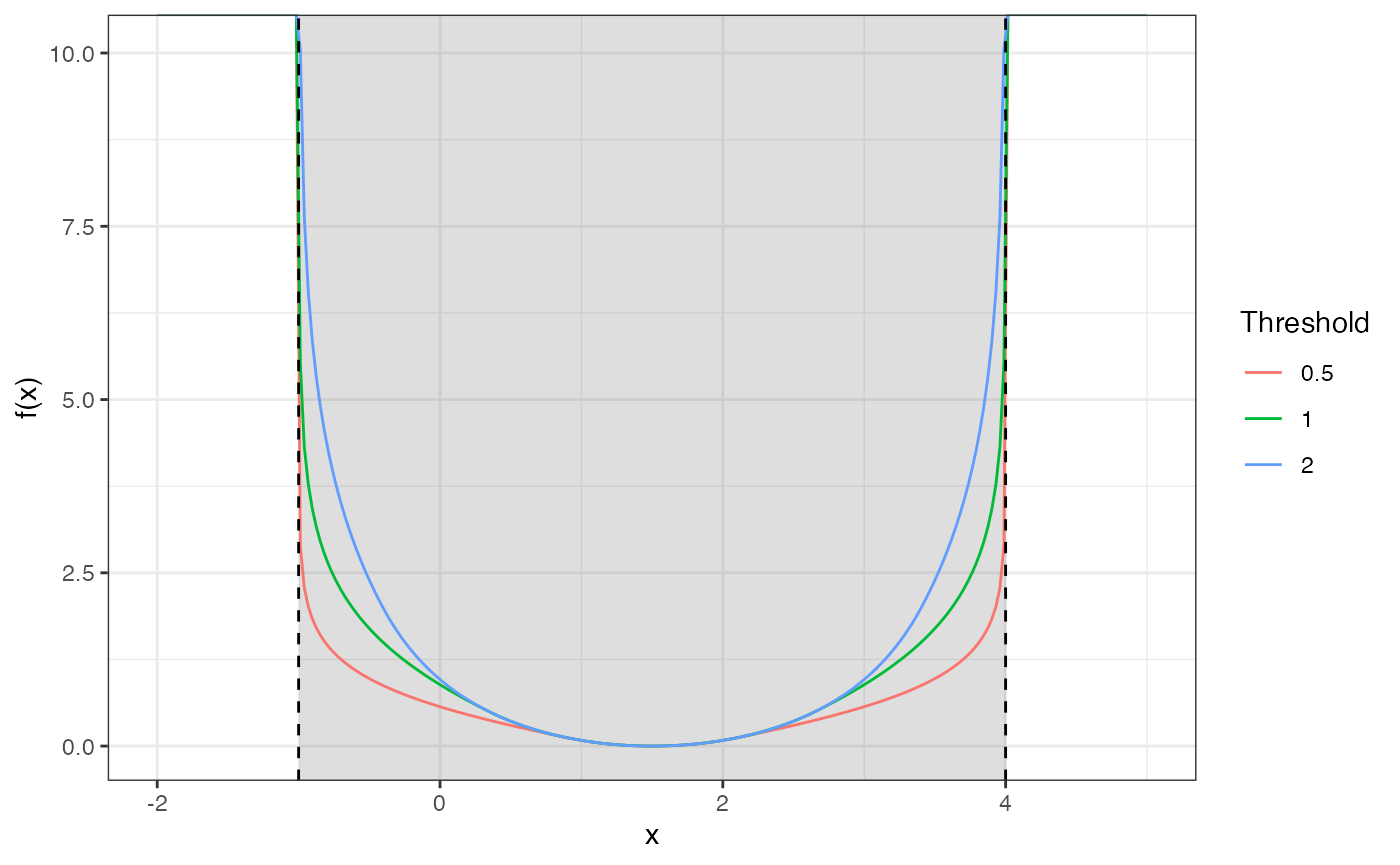

Comparison of Huber penalty functions with different thresholds.

lb <- -1
ub <- 4
tibble(
  x = seq(-2, 5, length.out = 250)
) |>
  rowwise() |>
  mutate(
    `0.5` = brlavaan:::pen_huber(x, lb = lb, ub = Inf, thres = 0.5),
    `1` = brlavaan:::pen_huber(x, lb = lb, ub = Inf, thres = 1),
    `2` = brlavaan:::pen_huber(x, lb = lb, ub = Inf, thres = 2)
  ) |> 
  pivot_longer(-x) |>
  ggplot(aes(x, value, color = name)) +
  # annotate("rect", xmin = lb, xmax = ub, ymin = -Inf, ymax = Inf, alpha = 0.2) +
  geom_line() +
  geom_vline(xintercept = c(lb), linetype = "dashed") +
  labs(y = "f(x)", col = "Threshold")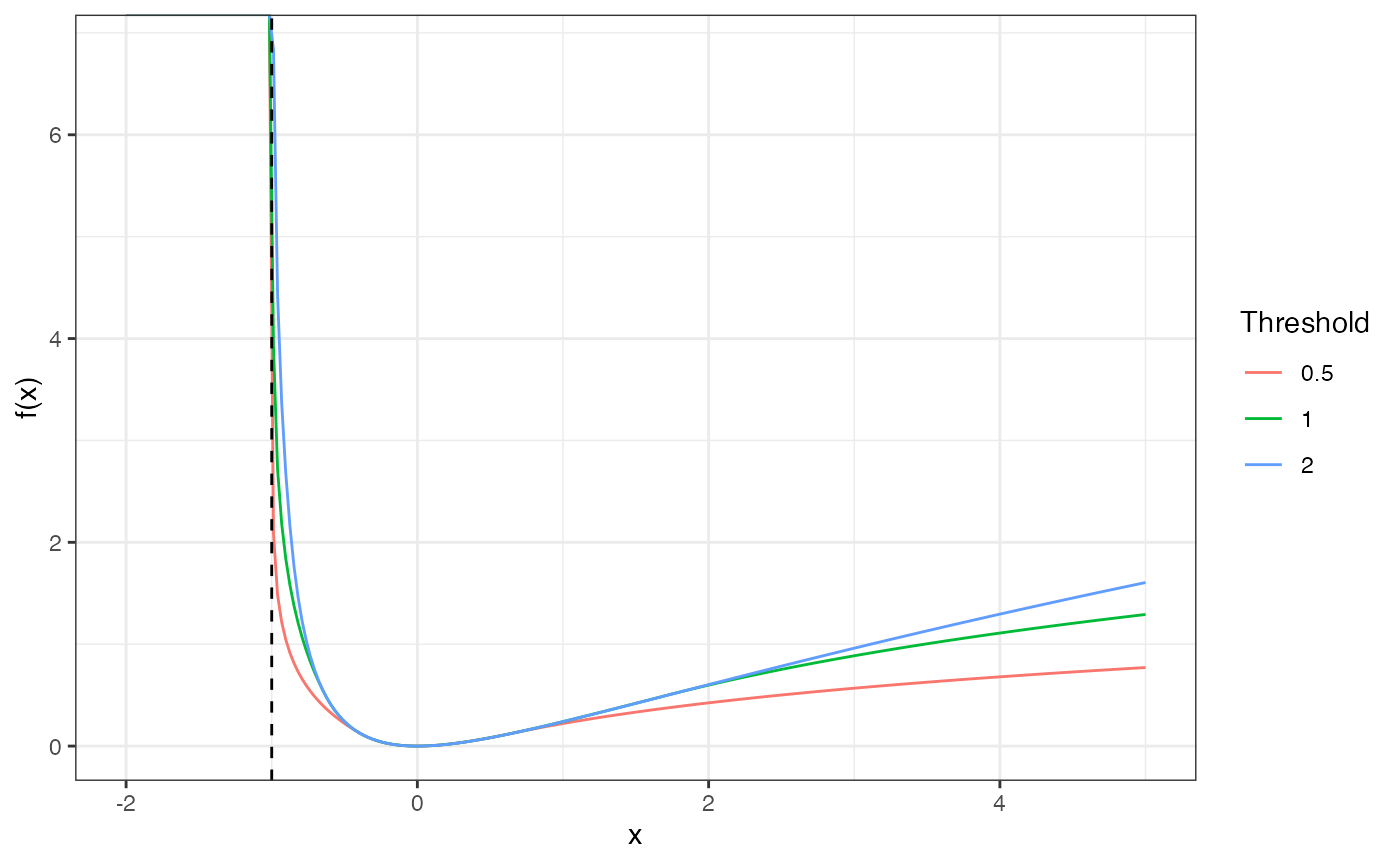

Comparison of left-bounded Huber penalty functions with different thresholds.

Creating your own plugin penalty function

To be developed…