Skip to contents

The basics

Source: vignettes/articles/basics.Rmd
basics.Rmd

Structural equation models

Let yi∈ℝpy_i\in \mathbb R^p, i=1,…,ni=1,\dots,n be independent multivariate data observations. A general form for structural equation models is the following: yi=ν+Ληi+ϵi, y_i = \nu + \Lambda \eta_i + \epsilon_i, {#eq-measurement} where the errors ϵi∼N(0,Θ)\epsilon_i \sim \operatorname{N}(0,\Theta) are assumed to be normally distributed, and the latent factors ηi\eta_i are related to each other through the structural part of the model: ηi=α+Bηi+ζi, \eta_i = \alpha + B \eta_i + \zeta_i, {#eq-structural} where ζi∼N(0,Ψ)\zeta_i \sim \operatorname{N}(0,\Psi) are the structural disturbances, and BB is a matrix of regression coefficients with 0 on the diagonals. The structural model can be rewritten as ηi=(I−B)−1α+(I−B)−1ζi\eta_i = (I - B)^{-1} \alpha + (I - B)^{-1} \zeta_i. Plugging this into @eq-measurement, we get the reduced form of the model, where each yi∼Np(μ,Σ)y_i \sim \operatorname{N}_p (\mu, \Sigma), with μ=μ(θ)=ν+Λ(I−B)−1αΣ=Σ(θ)=Λ(I−B)−1Ψ(I−B)−⊤Λ⊤+Θ. \begin{align} \mu &= \mu(\theta) = \nu + \Lambda (I - B)^{-1} \alpha \\ \Sigma &= \Sigma(\theta) = \Lambda(I - B)^{-1} \Psi (I - B)^{-\top} \Lambda^\top + \Theta. \end{align} We have denoted by θ∈ℝm\theta\in\mathbb R^m the collection of all free parameters (intercepts, loadings, regression coefficients, and variances) in the model. Evidently, the likelihood of the model is given by the multivariate normal density: ℓ(θ)=−np2log(2π)−n2log|Σ|−12∑i=1n(yi−μ)⊤Σ−1(yi−μ). \ell(\theta) = -\frac{np}{2}\log(2\pi) - \frac{n}{2}\log|\Sigma| - \frac{1}{2}\sum_{i=1}^n (y_i - \mu)^\top \Sigma^{-1} (y_i - \mu).

The gradient of the log-likelihood function with respect to a component of θ\theta appearing in the mean vector μ\mu is given by ∂ℓ∂θμ=∂ℓ∂μ∂μ∂θμ=∑i=1n(yi−μ)⊤Σ−1⋅∂μ∂θμ=n(y‾−μ)⊤Σ−1⋅∂μ∂θμ. \begin{align} \frac{\partial\ell}{\partial \theta_\mu} &= \frac{\partial\ell}{\partial \mu} \frac{\partial \mu}{\partial \theta_\mu} \\ &= \sum_{i=1}^n (y_i - \mu)^\top \Sigma^{-1} \cdot \frac{\partial \mu}{\partial \theta_\mu} \\ &= n (\bar y - \mu)^\top \Sigma^{-1} \cdot \frac{\partial \mu}{\partial \theta_\mu}. \end{align} The gradient of the log-likelihood function with respect to a component of θ\theta appearing in Σ\Sigma is given by ∂ℓ∂θσ=⟨∂ℓ∂Σ,∂Σ∂θσ⟩=⟨−n2Σ−1+n2Σ−1SΣ−1,∂Σ∂θσ⟩=⟨n2E,∂Σ∂θσ⟩,. \begin{align} \frac{\partial\ell}{\partial \theta_\sigma} &= \left\langle \frac{\partial\ell}{\partial \Sigma}, \frac{\partial \Sigma}{\partial \theta_\sigma} \right\rangle \\ &= \left\langle -\frac{n}{2} \Sigma^{-1} + \frac{n}{2} \Sigma^{-1}S\Sigma^{-1} , \frac{\partial \Sigma}{\partial \theta_\sigma} \right\rangle \\ &= \left\langle \frac{n}{2} E , \frac{\partial \Sigma}{\partial \theta_\sigma} \right\rangle, \end{align}. where SS is the (biased) sample covariance matrix, and E=Σ−1(S−Σ)Σ−1E = \Sigma^{-1}(S-\Sigma)\Sigma^{-1}.

Growth curve model

For the growth curve model, we have a latent intercept ii and slope ss (so q=2q=2). There are five parameters in the latent component: Two intercepts α1\alpha_1 and α2\alpha_2, and the three unique variances and covariances Ψ11\Psi_{11}, Ψ22\Psi_{22}, and Ψ12\Psi_{12}. The loadings for the “intercept” latent variable are all fixed to 1, whereas the loadings for the “slope” latent variable increment from 0 to 9. Thus, Λ\Lambda is some fixed 10×210 \times 2 matrix. Furthermore, the observed variables yjy_j, j=1,…,pj=1,\dots,p share a common residual error variance vv. In total, there are six parameters to be estimated in the model (in this order): θ=(Ψ11,α1,Ψ22,α2,Ψ12,v)\theta = (\Psi_{11}, \alpha_1, \Psi_{22}, \alpha_2, \Psi_{12}, v).

Reliability = 0.8 Reliability = 0.5
α1\alpha_1 0 0
α2\alpha_2 0 0
Ψ1,1\Psi_{1,1} 550 275
Ψ2,2\Psi_{2,2} 100 50
Ψ1,2\Psi_{1,2} 40 20
vv 500 1300

For the growth curve model, the gradients are simplified somewhat:

  • ∂ℓ(θ)∂α=nΛ⊤Σ−1(y‾−μ)\frac{\partial\ell(\theta)}{\partial \alpha} = n \Lambda^\top \Sigma^{-1} (\bar y - \mu)
  • ∂ℓ∂Ψij=n2tr{Λ⊤EΛ∂Ψ∂Ψij}\frac{\partial\ell}{\partial \Psi_{ij}} = \frac{n}{2} \operatorname{tr} \left\{\Lambda^\top E \Lambda \frac{\partial \Psi}{\partial \Psi_{ij}} \right\}
  • ∂ℓ∂v=n2tr(E)\frac{\partial\ell}{\partial v} = \frac{n}{2} \operatorname{tr}(E)

The implementation in R code is also straightforward (see R/40-manual_growth.R). Compare the behaviour of the eBR and iBR methods using lavaan’s internals (via fit_sem()) and using manual functions (via fit_growth()).

library(tictoc)
set.seed(26)
dat <- gen_data_growth(n = 15, rel = 0.5, dist = "Normal", scale = 1 / 10)
mod <- txt_mod_growth(0.5)
tru <- truth(dat)

tic.clearlog()
fit <- list()

tic("ML: lavaan")
fit$lav <- growth(mod, dat, start = tru)
toc(log = TRUE)
#> ML: lavaan: 0.151 sec elapsed

tic("ML: brlavaan")
fit$ML <- fit_sem(mod, dat, "none", lavfun = "growth", start = tru)
toc(log = TRUE)
#> ML: brlavaan: 0.024 sec elapsed
tic("eBR: brlavaan")
fit$eBR <- fit_sem(mod, dat, "explicit", lavfun = "growth", start = tru)
toc(log = TRUE)
#> eBR: brlavaan: 0.332 sec elapsed
tic("iBR: brlavaan")
fit$iBR <- fit_sem(mod, dat, "implicit", lavfun = "growth", start = tru)
toc(log = TRUE)
#> iBR: brlavaan: 1.307 sec elapsed

tic("ML: manual")
fit$MLman <- fit_growth(mod, dat, "none", start = tru[1:6])
toc(log = TRUE)
#> ML: manual: 0.01 sec elapsed
tic("eBR: manual")
fit$eBRman <- fit_growth(mod, dat, "explicit", start = tru[1:6])
toc(log = TRUE)
#> eBR: manual: 0.521 sec elapsed
tic("iBR: manual")
fit$iBRman <- fit_growth(mod, dat, "implicit", start = tru[1:6])
toc(log = TRUE)
#> iBR: manual: 1.469 sec elapsed

# Compare
c(list(truth = tru[1:6]), lapply(fit, \(x) round(coef(x)[1:6], 5)))
#> $truth
#>  i~~i   i~1  s~~s   s~1  i~~s     v 
#>  2.75  0.00  0.50  0.00  0.20 13.00 
#> 
#> $lav
#>     i~~i      i~1     s~~s      s~1     i~~s        v 
#>  3.84160  0.18158  0.78045 -0.12988 -0.52747 12.75903 
#> 
#> $ML
#>     i~~i      i~1     s~~s      s~1     i~~s        v 
#>  3.84163  0.18157  0.78045 -0.12988 -0.52748 12.75907 
#> 
#> $eBR
#>     i~~i      i~1     s~~s      s~1     i~~s        v 
#>  4.39245  0.18153  0.84284 -0.12985 -0.60927 12.75897 
#> 
#> $iBR
#>     i~~i      i~1     s~~s      s~1     i~~s        v 
#>  4.28355  0.18157  0.82938 -0.12988 -0.59457 12.75902 
#> 
#> $MLman
#>     i~~i      i~1     s~~s      s~1     i~~s        v 
#>  3.84163  0.18157  0.78045 -0.12988 -0.52748 12.75907 
#> 
#> $eBRman
#>     i~~i      i~1     s~~s      s~1     i~~s        v 
#>  4.39159  0.18154  0.84279 -0.12988 -0.60903 12.75906 
#> 
#> $iBRman
#>     i~~i      i~1     s~~s      s~1     i~~s        v 
#>  4.28353  0.18157  0.82939 -0.12988 -0.59459 12.75893
sapply(fit, \(x) if (inherits(x, "lavaan")) x@optim$converged else x$converged)
#>    lav     ML    eBR    iBR  MLman eBRman iBRman 
#>   TRUE   TRUE   TRUE   TRUE   TRUE   TRUE   TRUE

Two factor model

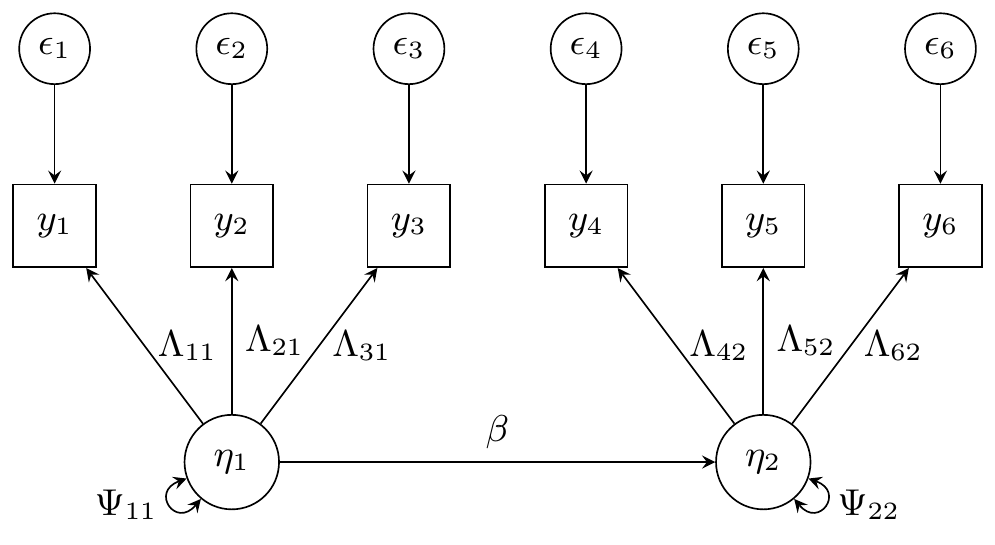
For the two factor model, we have two latent variables η1\eta_1 and η2\eta_2, each indicated by three observed variables, (y1,y2,y3)(y_1, y_2, y_3) and (y4,y5,y6)(y_4, y_5, y_6) respectively. Each observed variable has a corresponding error ϵj∼N(0,Θj,j)\epsilon_j \sim N(0, \Theta_{j,j}), leading to six variance parameters. The latent variables have a regression path from η1\eta_1 to η2\eta_2 with parameter β\beta, and each have a variance parameter Ψ11\Psi_{11} and Ψ22\Psi_{22} respectively. For the factor loadings, we fix Λ11\Lambda_{11} and Λ42\Lambda_{42} to 11 for identifiability. The thirteen parameters to be estimated in the two factor model are θ=(Λ21,Λ31,Λ52,Λ62,β,Θ11,Θ22,Θ33,Θ44,Θ55,Θ66,Ψ11,Ψ22)\theta = (\Lambda_{21}, \Lambda_{31}, \Lambda_{52}, \Lambda_{62}, \beta, \Theta_{11}, \Theta_{22}, \Theta_{33}, \Theta_{44}, \Theta_{55}, \Theta_{66}, \Psi_{11}, \Psi_{22}). (In this order in the code).

Reliability = 0.8 Reliability = 0.5
Λ2,1\Lambda_{2,1} 0.7 0.7
Λ3,1\Lambda_{3,1} 0.6 0.6
Λ5,2\Lambda_{5,2} 0.7 0.7
Λ6,2\Lambda_{6,2} 0.6 0.6
β\beta 0.25 0.25
Θ1,1\Theta_{1,1} 0.25 1
Θ2,2\Theta_{2,2} 0.1225 0.49
Θ3,3\Theta_{3,3} 0.09 0.36
Θ4,4\Theta_{4,4} 0.25 1
Θ5,5\Theta_{5,5} 0.1225 0.49
Θ6,6\Theta_{6,6} 0.09 0.36
Ψ1,1\Psi_{1,1} 1 1
Ψ2,2\Psi_{2,2} 1 1

Due to diagonal matrices, we express the covariance parameters as the diagonal of the covariance matrices, which have all other entries as zero.

  • ∂ℓ∂Λij=ntr{MΛ⊤E∂Λ∂Λij}=n[MΛ⊤E]ji\frac{\partial \ell}{\partial \Lambda_{ij}} = n \operatorname{tr}\left\{ M \Lambda^\top E \frac{\partial\Lambda}{\partial \Lambda_{ij}} \right\} = n[M\Lambda^\top E]_{j i}
  • ∂ℓ∂β=ntr{Ψ(I+B⊤)Λ⊤EΛ∂B∂β}=n[Ψ(I+B⊤)Λ⊤EΛ]12\frac{\partial \ell}{\partial \beta} = n \operatorname{tr}\left\{ \Psi (I + B^\top) \Lambda^\top E \Lambda \frac{\partial B}{\partial \beta} \right\} = n[\Psi (I + B^\top) \Lambda^\top E \Lambda]_{12}
  • ∂ℓ∂diag(Θ)=n2diag(E)\frac{\partial \ell}{\partial \text{diag}(\Theta)} = \frac{n}{2}\text{diag}(E)
  • ∂ℓ∂diag(Ψ)=n2diag((I−B)−⊤Λ⊤EΛ(I−B)−1)\frac{\partial \ell}{\partial \text{diag}(\Psi)} = \frac{n}{2}\text{diag}\left((I - B)^{-\top}\Lambda^\top E \Lambda (I-B)^{-1}\right)

We have M=(I−B)−1Ψ(I−B)−⊤M = (I - B)^{-1} \Psi (I - B)^{-\top}.